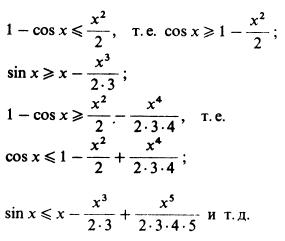Неравенства

Неравенство — это два числа или математических выражения, соединенных одним из знаков: > (больше), < (меньше), ≥ (больше или равно), ≤ (меньше или равно). Запись a > b означает то же, что b < a, так что наличие двух противоположных знаков неравенства — просто дополнительное удобство. Неравенства, содержащие знак > или <, называют строгими, а содержащие знак ≥ или ≤ — нестрогими.

Числовое неравенство может быть верным или неверным; например, неравенства 2⁷ > 5³; 40/77 < 13/25; √2 ≥ 1,4142; 5 ≤ 5; −1 ≤ 0 верны, а π > 355/113 неверно. Таким образом, с точки зрения математической логики неравенство является высказыванием. Неравенство с переменными (т.е. неравенство, в запись которого входят буквы, принимающие разные значения) может при одних значениях переменных быть верным, при других — нет. Доказать такое неравенство — значит доказать, что оно выполнено при всех допустимых значениях переменных (такие неравенства называются тождественными). Для неравенства с переменными можно поставить задачу: решить неравенство, т. е. описать множество значений переменных, при которых оно выполнено.

Решая или доказывая неравенства, мы опираемся на основные свойства отношения «больше-меньше» между числами:

(1) отношение неравенства антисимметрично, т. е. для любых различных чисел a и b либо a > b, либо b > a, и транзитивно, т. е. для любых трех чисел a, b и c если a > b и b > c, то a > c;

(2) если a > b, то a+c > b+c при любом c;

(3) если a > b и c > 0, то a•c > b•c.

Из последних двух свойств, связывающих отношение неравенства между числами с арифметическими операциями, именно свойство (3) вызывает наибольшее число ошибок у начинающих: часто забывают, что при умножении на отрицательное число неравенство изменяется на противоположное. Из основных свойств (1), (2), (3) можно вывести все другие: если a < b и c < d, то a+c < b+d (правило почленного сложения неравенств); если 0 < a < b, n — натуральное число, то aⁿ < bⁿ и т. п.

При расширении понятия числа — переходя от целых чисел к рациональным, затем к действительным — мы должны определять отношение «больше-меньше» на новом множестве так, чтобы сохранялись основные его свойства. По определению из двух дробей p/q и m/n (с положительными знаменателями q, n) первая больше, если pn > mq; из двух положительных бесконечных десятичных дробей больше та, у которой больше единиц в самом левом из несовпадающих разрядов (при этом не рассматриваются дроби с окончаниями 9999…).

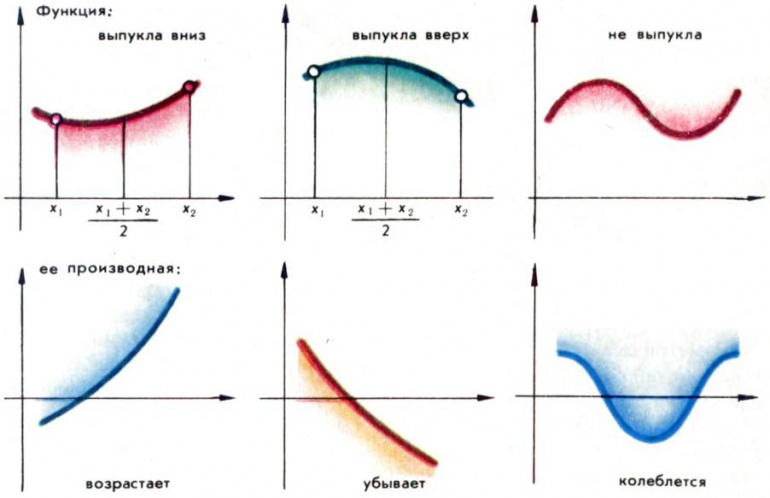
С помощью неравенств задаются основные числовые множества (отрезок a ≤ x ≤ b, интервал a < x < b, луч x > a и т.д.), формулируются определения предела, непрерывной функции, монотонной последовательности и функции, целого ряда других важных понятий. Например, определение выпуклой функции y=f (x) можно сформулировать так: непрерывная функция называется выпуклой вниз, если для всех x₁, x₂ выполнено неравенство

а выпуклой вверх — если верно неравенство противоположного смысла (см. Выпуклые функции); для функции, имеющей производную, это эквивалентно тому, что у = f '(x) — монотонная функция (соответственно неубывающая или невозрастающая, рис. 1).

Рис. 1. Выпуклые функции и их производные.

На языке неравенств нередко формулируется постановка задачи во многих приложениях математики. Например, многие экономические задачи сводятся к исследованию систем линейных неравенств с большим числом переменных (см. Геометрия). Часто то или иное неравенство служит важным вспомогательным средством, основной леммой, позволяющей доказать или опровергнуть существование каких-то объектов (скажем, решений уравнения), оценить их количество, провести классификацию. Например, чтобы классифицировать все правильные многогранники, нужно прежде всего вспомнить, какие углы могут иметь правильные многоугольники, и воспользоваться неравенством: сумма величин плоских углов выпуклого многогранного угла не больше 360°.

Эта теорема наряду с самыми первыми геометрическими неравенствами («перпендикуляр меньше наклонной, проведенной из одной и той же точки к данной прямой», «сторона треугольника меньше суммы двух других сторон», «против большего угла треугольника лежит большая сторона») принадлежит еще древнегреческой математике — она содержалась в знаменитых «Началах» Евклида.

Неравенства — это не только вспомогательный инструмент. В каждой области математики — алгебре и теории чисел (см. Чисел теория), геометрии и топологии, теории вероятностей и теории функций, математической физике и теории дифференциальных уравнений, теории информации и дискретной математике — можно указать фундаментальные результаты, формулируемые в виде неравенств.

Во многих разделах математики, особенно в математическом анализе, в прикладной математике, неравенства встречаются значительно чаще, чем равенства. Скажем, решение каких-то практически важных уравнений лишь по счастливой случайности удается найти точно — в виде числа или формулы, а для приближенного решения в математике всегда требуется указать оценку погрешности, т. е. доказать некоторое неравенство. В этом заключается одно из главных отличий между математическим и физическим уровнем строгости: физик готов ограничиться нахождением «порядка величины» там, где математик стремится строго доказать какие-то оценки, т. е. неравенства.

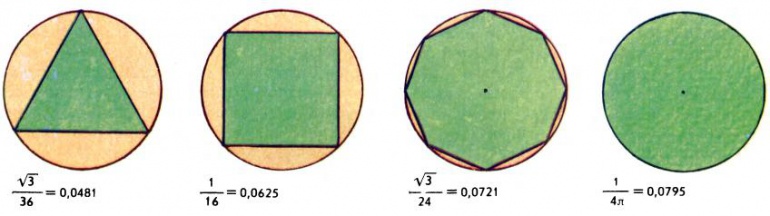
Находя оценку той или иной величины сверху (максимум) или снизу (минимум), т. е. доказывая, что эта величина не больше какого-то числа M (или не меньше m), мы стараемся получить как можно более точный результат: оценку сверху — пониже, снизу — повыше. Самая точная возможная оценка числового множества A сверху обозначается sup A (супремум A). Аналогично определяется самая точная оценка снизу: inf A (инфинум A). Рассмотрим, для примера, отношение площади S многоугольника к квадрату его периметра P. Чем более «округлый» многоугольник, тем величина S/P² больше — в этом легко убедиться на примерах (рис. 2). Точная верхняя грань этого отношения: sup S/P² = 1/(4π). На множестве всех многоугольников эта оценка не достигается — нет такого многоугольника, для которого S/P² в точности равно 1/(4π); а на множестве всех (выпуклых) фигур — достигается, причем только для круга радиуса R это отношение как раз равно πR²/(2πR)² = 1/(4π). Когда величина достигает своего наибольшего значения, вместо sup можно писать max (максимум); соответственно вместо inf писать min (минимум).

Рис. 2. Отношение площади к квадрату периметра максимально для круга.

Доказательство неравенств тесно связано с исследованием функций на экстремум (см. Экстремум функции). Чтобы доказать, что максимум какой-то функции f равен M, мы должны указать значения аргументов, при которых функция f равна М, и доказать неравенство M. Например, тот факт, что на множестве всех фигур S/P² < 1/(4π), обычно формулируется так: из всех фигур данного периметра наибольшую площадь имеет круг. Это знаменитое изопериметрическое неравенство (доказанное впервые Л. Эйлером) — представитель целого класса геометрических неравенств, различные варианты и многомерные обобщения которых используются в разных отделах математики и ее приложениях.

Важная часть работы математика — доказательство тождественных неравенств, т. е. таких, которые верны при всех значениях входящих в них переменных (или при всех заранее оговоренных допустимых значениях переменных). Иногда это дело несложное — например, чтобы доказать неравенство f > g, где f и g — некоторые функции, удается преобразовать разность f − g так, что становится очевидной ее положительность: a² + b² ≥ 2ab, поскольку (a − b)² ≥ 0; a² + b² + c² ≥ ab + bc + ca , поскольку (a − b)² + (b − c)² + (c − a)² ≥ 0.

Но бывает, что для доказательства неравенства приходится использовать весьма тонкие геометрические или аналитические соображения. Как опытному шахматисту помогает знание основных дебютов, так и математику полезно знать некоторые часто встречающиеся классические тождественные неравенства. Среди них — красивые неравенства, в которые переменные входят симметричным образом (см. Средние значения).

Серию таких неравенств дает следующее общее неравенство датского математика И. Йенсена (1859—1925) для выпуклых функций: если f — выпуклая вниз функция на отрезке [a, b] и p₁, p₁, …, p_n — любые положительные числа, то при всех x₁, x₂, …, x_n из [a, b]

Для выпуклой вверх функции верно обратное неравенство; в частности, при f (x) = log x, p₁ = p₂ = … = p_n = 1/n, x_i > 0 (i = 1, …, n), отсюда получается неравенство для среднего арифметического и среднего геометрического.

Рис. 3. Центр масс системы грузов имеет координаты.

Рис. 4. Гипербола y = 1/x.

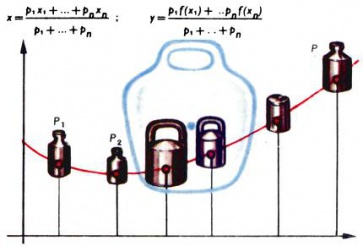
Наглядное объяснение этого неравенства состоит в следующем: если на графике выпуклой вниз функции расположить грузы с произвольными массами p₁, p₂, …, p_n, то центр их масс будет лежать выше графика (рис. 3).

Для получения оценок сумм вида f (1) + f (2) + … + f (n) применяются метод математической индукции, а также сравнение этой суммы со специально подобранным интегралом. Например, для суммы

h_n = 1 + 1/2 + … + 1/n

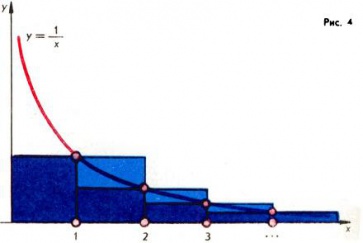
(см. Гармонический ряд) сравнение её с площадью под гиперболой y = 1/x (рис. 4) дает оценки: ln n < h_n < ln n + 1. Скажем, при n = 1000, отсюда получаем 6,9 < h₁₀₀₀ < 7,91.

Доказательства непрерывности и дифференцируемости элементарных функций, формул для их производных опираются на некоторые основные неравенства; среди них — неравенства sin x < x < tg x (при 0 < x < π/2), e^x > 1 + x, неравенство Бернулли (1 + x)ⁿ ≥ 1 + nx (при x > −1, натуральном n).

Методы математического анализа, в свою очередь, удобное средство доказательства неравенств для функций от одной переменной. Так, если значения двух функций f (x) и g (x) совпадают при x = a и f '(x) ≤ g '(x) при x ≥ a, то f (b) > g (b) при любом b ≥ a, другими словами, неравенство можно почленно интегрировать. Приведем один пример, показывающий, как это соображение позволяет вычислять с большой точностью sin x.

Поскольку cos x ≤ 1 и (sin x)' = cos x, то при x > 0

Точно так же отсюда получаем последовательно:

Таким образом, мы получаем, что sin x заключен между суммой первых k и первых k + 1 членов ряда

(где n! = 1•2• … •n)

(при любом k = 1, 2, …); точно так же для cos x аналогичные оценки дает ряд

Мы говорили выше о способах получения тождественных неравенств. Если же записано какое-то неравенство вида

f (x) > g (x),

где f и g — любые функции, x — переменная, то при некоторых значениях х оно будет верно, при других — нет.

Решить такое неравенство — значит найти множество X всех значений переменной x, при которых оно верно. Задачи на решение неравенств подробно изучаются в школьном курсе. Между решением неравенств и решением уравнений много общего — неравенства тоже нужно с помощью преобразований сводить к более простым. Важное отличие состоит в том, что множество X решений неравенства, как правило, бесконечно (отрезок, луч, объединение нескольких отрезков). Сделать полную проверку ответа в этом случае нельзя. Поэтому, решая неравенство, нужно обязательно переходить к эквивалентному ему неравенству — имеющему в точности то же множество решений. Для этого, опираясь на основные свойства неравенств, надо проделывать лишь такие преобразования, которые сохраняют знак неравенства и обратимы. Скажем, можно применить к обеим частям операцию возвышения в куб, но нельзя — операции возвышения в квадрат (если только не известно, что обе части его заведомо положительны); вообще неравенства f < g и F (f) < F (g) эквивалентны, если функция F неубывающая.

Однако если мы умеем решать уравнение f (x) = g (x), то решить неравенство f (x) > g (x), как правило, не представляет труда: в этом помогает «метод интервалов». Будем говорить о неравенстве вида f (x) > 0 (мы можем перенести все члены в левую часть). Пусть функция f определена и непрерывна на всей прямой или на области D, состоящей из нескольких (конечных или бесконечных) отрезков. Так будет для всех элементарных функций. Отметим корни уравнения f (x) = 0; они разбивают область определения функции f на ряд интервалов, в каждом из которых f сохраняет знак. Какой именно знак имеет f (x) в каждом из интервалов, можно выяснить, подставив в f (x) одно (любое) значение х из этого интервала. Остается выбрать те интервалы, в которых f (x) положительно, — это будет искомое множество X.

Например, чтобы решить неравенство

заметим, что знаменатель x³ − 2x + 1 = (x − 1)(x² + x − 1) обращается в 0 при x = (−1 ± √5)/2 и x = 1, а вся дробь обращается в 1 при x = 0 и x = 2. Остается на каждом из 6 кусочков, на которые делят прямую эти пять точек, найти знак дроби

как это и бывает обычно (кроме исключительных случаев «кратных корней»), знаки чередуются. (Ответ: X состоит из трех множеств: x < (−1 − √5)/2, 0 < x < (−1 + √5)/2 и 1 < x < 2)

Рис. 5. Множество решений — объединение отрезков.

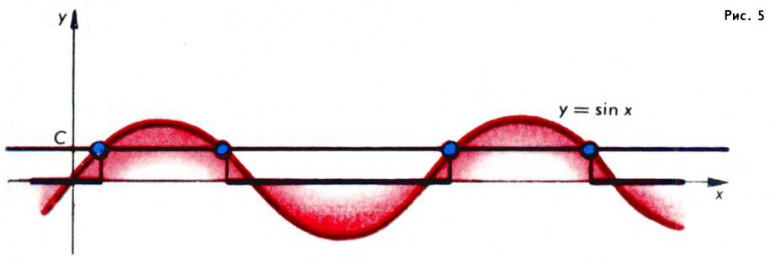
Еще проще применять «метод интервалов», если заранее известно, где функция убывает, а где — возрастает, и известен ее график. Например, неравенство sin x ≤ c будет выполнено на отрезках между корнями x = (−1)ⁿ arcsin x + πn уравнения sin x = c (здесь |c| ≤ 1), содержащих точки −π/2 + 2πn. На рис. 5 множество решений — объединение отрезков [−arcsin c + (2n − 1)π; arcsin c + 2πn], n = 0, ±1, … .