Уравнение
Уравнение — это два выражения, соединенные знаком равенства; в эти выражения входят одна или несколько переменных, называемых неизвестными. Решить уравнение — значит найти все значения неизвестных, при которых оно обращается в верное равенство, или установить, что таких значений нет.
В школьном курсе, как правило, рассматривают уравнения, в которых неизвестные принимают числовые значения. Числовое значение неизвестного, удовлетворяющее уравнению с одним неизвестным, называется корнем или решением этого уравнения. Набор чисел, удовлетворяющих уравнению с несколькими неизвестными, называется его решением.
<addc>G</addc>
В математике рассматривают также уравнения, в которых неизвестными являются целые числа (диофантовы уравнения), векторы (векторные уравнения), функции (дифференциальные, интегральные, функциональные уравнения) и объекты другой природы. Вместе с уравнением указывают его область определения (множество допустимых значений неизвестных); если это не сделано, то предполагается, что это — естественная общая область определения выражений, стоящих в левой и правой частях уравнения.
Уравнение — одно из важнейших понятий математики. В большинстве практических и научных задач, где какую‑то величину нельзя непосредственно измерить или вычислить по готовой формуле, удается составить соотношение (или несколько соотношений), которым оно удовлетворяет. Так получают уравнение (или систему уравнений) для определения неизвестной величины.
Развитие методов решения уравнений, начиная с зарождения математики как науки, долгое время было основным предметом изучения алгебры. Привычная нам буквенная запись уравнений окончательно сложилась в XVI в.; традиция обозначать неизвестные последними буквами латинского алфавита [math]x,y,z,…,[/math] а известные величины (параметры) — первыми [math]a,b,c,…[/math] идет от французского ученого Р. Декарта.
Обычный путь алгебраического (чаще говорят, аналитического) решения уравнения состоит в том, что с помощью преобразований его сводят к более простым уравнениям. Если все решения одного уравнения являются решениями другого, то второе уравнение называется следствием первого. Если каждое из двух уравнений — следствие другого (т. е. множества их решений совпадают), то такие уравнения называются равносильными. Применяя к обеим частям уравнения одно и то же преобразование, мы приходим к следствию этого уравнения. Если же это преобразование обратимо, то получается уравнение, равносильное данному. (Например, умножая обе части уравнения на одно и то же число, мы получаем следствие данного уравнения. Если это число отлично от нуля, то выполненное преобразование обратимо, так что полученное уравнение равносильно исходному).
Решая уравнение с одним неизвестным, мы пытаемся прийти к простейшим уравнениям, для решения которых есть готовые формулы. Это линейные уравнения, квадратные уравнения, уравнения вида [math]φ(x)=c[/math], где [math]c[/math] — число, а [math]φ[/math] — одна из основных элементарных функций: степенная [math]\varphi (x)={{x}^{n}}[/math], показательная [math]\varphi (x)={{a}^{x}}[/math], логарифмическая [math]\varphi (x)={{\log }_{a}}x[/math], тригонометрические [math]\varphi (x)=\sin x[/math], [math]\varphi (x)=\cos x[/math], [math]\varphi (x)=\mathrm{tg}\, x[/math].
Заметим, что запись общего решения уравнения [math]φ(x)=c[/math] требует введения функции [math]ψ[/math], обратной к функции [math]φ[/math]. Если [math]\varphi (x)={{x}^{n}}[/math], то [math]\psi (c)=\sqrt[n]{c}[/math]; если [math]\varphi (x)={{a}^{x}}[/math], то [math]\psi (c)={{\log }_{a}}c[/math]; если [math]\varphi (x)=\sin x[/math] и [math]−π/2≤x≤π/2[/math], то [math]\psi (c)=\arcsin x[/math].
Как же сводятся уравнения к простейшим? Для конкретного типа уравнений (алгебраических, тригонометрических, иррациональных, показательных, логарифмических и т.п.) разработаны частные приемы решения. Из общих методов решения уравнений остановимся на трех, которые встречаются чаще всего.
Если левую часть уравнения [math]f(x)=0[/math] удается разложить на множители: [math]f(x)={{f}_{1}}(x)\cdot \ldots \cdot {{f}_{m}}(x),[/math] то оно распадается на уравнения [math]{{f}_{1}}(x)=0,[/math] [math]{{f}_{2}}(x)=0 …,[/math] [math]{{f}_{1}}(x)=0,[/math] объединение множеств их решений дает множество решений данного уравнения. Например, уравнение [math]{{x}^{3}}-7x+6=0[/math] можно решить так: [math]({{x}^{3}}-x)-(6x-6)=0,[/math] [math]x(x-1)(x+1)-6(x-1)=0,[/math] [math](x-1)({{x}^{2}}+x-6)=0.[/math] Решая уравнения [math]x−1=0[/math] и [math]{{x}^{2}}+x-6=0,[/math] находим все корни данного уравнения: [math]1, 2[/math] и [math]−3.[/math] Этот метод принято называть методом разложения на множители.
Часто удается упростить уравнение, принимая в качестве новой неизвестной некоторую функцию от старой неизвестной. Например, уравнение [math]\sin x+\cos x=\sin 2x[/math] можно свести к квадратному уравнению, положив [math]y=\sin x+\cos x.[/math] Тогда [math]\sin 2x={{y}^{2}}-1,[/math] и мы приходим к уравнению [math]{{y}^{2}}-y-1=0.[/math]
Иногда удается решить уравнение, анализируя функциональные свойства его левой и правой частей.
Например, так как левая часть уравнения [math]{{2}^{x}}+{{3}^{x}}=5[/math] возрастает, а правая — постоянна, то это уравнение не может иметь более одного корня. Единственный корень [math]x=1[/math] легко угадывается.
Решая уравнение [math]{{\sin }^{3}}x+{{\cos }^{5}}x=\sqrt{2},[/math] заметим, что при всех [math]x[/math] выполняются неравенства [math]{{\sin }^{3}}x\le {{\sin }^{2}}x,[/math] [math]co{{s}^{5}}x\le {{\cos }^{2}}x,[/math] откуда [math]si{{n}^{3}}x+{{\cos }^{5}}x\le [/math] [math]{{\sin }^{2}}x+{{\cos }^{2}}x=1,[/math] а так как [math]\sqrt{2}\gt 1,[/math] то данное уравнение не имеет корней.
До сих пор мы разбирали приемы решения уравнений, позволяющие найти корень уравнения как число или комбинацию известных функций от параметров. Однако далеко не все уравнения, возникающие на практике, можно решить подобным образом. Например, в начале XIX в. было доказано, что не существует общей формулы для решения алгебраических уравнений начиная с пятой степени. Да и в тех случаях, когда уравнение удается решить, формула для корней может быть чересчур громоздкой. Поэтому в математике разработаны различные методы приближенного решения уравнений. Простейший из них основан на том, что если функция [math]f(x)[/math] непрерывна во всех точках отрезка [math][a;b][/math] и принимает на его концах значения разных знаков, то уравнение [math]f(x)=0[/math] имеет на этом отрезке корень.
Приближенное решение уравнений тесно связано с построением графиков функций.
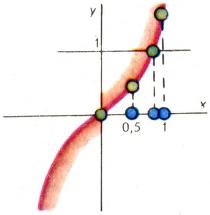
Например, построив график функции [math]y={{x}^{3}}+x,[/math] мы можем заключить, что уравнение [math]{{x}^{3}}+x=1[/math] имеет один корень и этот корень лежит на отрезке [math][0,5;1][/math], более точно — на отрезке [math][0,6;0,7][/math], еще более точно — на отрезке [math][0,682;0,683][/math] (рис. 1). Эта информация практически более полезна, чем точная формула Кардано, выражающая этот корень:
[math]\sqrt[3]{\frac{1}{2}+\sqrt{\frac{1}{4}+\frac{1}{27}}}+\sqrt[3]{\frac{1}{2}-\sqrt{\frac{1}{4}+\frac{1}{27}}}[/math]
(все равно извлекать радикалы можно лишь приближенно). Для отыскания корней с любой степенью точности» существуют «быстрые» алгоритмы, основанные на методе последовательных приближений (см. Приближенные вычисления).
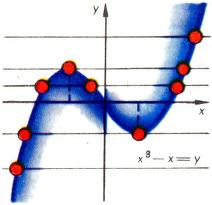
С помощью графика особенно удобно проводить исследование уравнений; например, по графику [math]y={{x}^{3}}-x[/math] (рис. 2) мы сразу видим, что уравнение [math]{{x}^{3}}-x=c[/math] имеет три корня при [math]\left| c \right|\lt 2/\sqrt{3},[/math] два — при [math]\left| c \right|=2/\sqrt{3}[/math] и один — при [math]\left| c \right|\gt 2/\sqrt{3}.[/math]