Квадратный трёхчлен
Так называют многочлен, определяемый формулой [math]a{{x}^{2}}+bx+c[/math] [math](a\ne 0).[/math] Числа [math]a, b[/math] и [math]c[/math] — коэффициенты квадратного трехчлена, они обычно называются: a — старший, b — второй или средний коэффициент, c — свободный член. Функция вида y = ax2 + bx + c называется квадратичной функцией.
После линейной функции квадратичная функция — простейшая и важнейшая элементарная функция. Многие физические зависимости выражаются квадратичной функцией; например, камень, брошенный вверх со скоростью v0, находится в момент времени t на расстоянии
[math]s(t)=-\frac{g}{2}{{t}^{2}}+{{v}_{0}}t[/math]
от земной поверхности (здесь g — ускорение силы тяжести); количество тепла Q, выделяемого при прохождении тока в проводнике с сопротивлением R, выражается через силу тока I формулой Q = RI2.
Квадратный трёхчлен. Рис. 1.
Квадратный трёхчлен. Рис. 2.
Квадратный трёхчлен. Рис. 3.
Квадратный трёхчлен. Рис. 4.
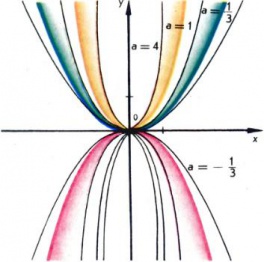
Простейший частный случай квадратичной функции есть функция y = ax2. На рис. 1 изображены графики функций y = ax2 при разных значениях a. График функции y = ax2 называется параболой.
У всех этих парабол вершина находится в начале координат; при a > 0 это наинизшая точка графика (наименьшее значение функции), а при a < 0, наоборот, наивысшая точка (наибольшее значение функции). Ось Oy есть ось симметрии каждой из таких парабол.
Как видно, при a > 0 парабола направлена вверх, при a < 0 — вниз.
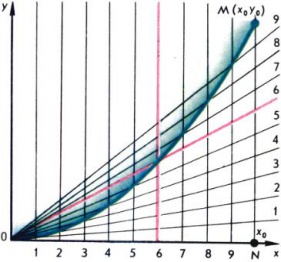
Существует простой и удобный графический способ, позволяющий строить любое число точек параболы y = ax2 без вычислений, если известна точка параболы, отличная от вершины. Пусть точка M(x0, y0) лежит на параболе y = ax2 (рис. 2). Если мы хотим построить между точками O и M дополнительно еще n точек, то делим отрезок ON оси абсцисс на n + 1 равных частей и в точках деления проводим перпендикуляры к оси Ox. На столько же равных частей делим отрезок NM и точки деления соединяем лучами с началом координат. Искомые точки параболы лежат на пересечении перпендикуляров и лучей с одинаковыми номерами (на рис. 2 число точек деления равно 9).
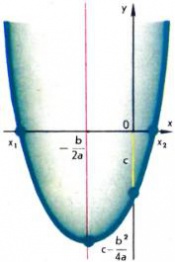
График функции y =ax2 + bx + c отличается от графика y = ax2 лишь своим положением и может быть получен просто перемещением кривой на чертеже. Это следует из представления квадратного трехчлена в виде
откуда легко заключить, что график функции y = ax2 + bx + c есть парабола y = ax2, вершина которой перенесена в точку
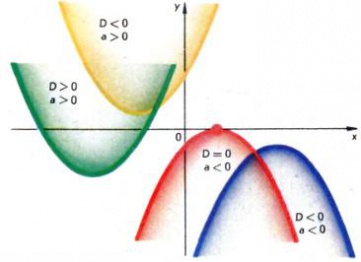
а ось её симметрии осталась параллельной оси Oy (рис. 3). Из полученного выражения для квадратного трехчлена легко следуют все его основные свойства. Выражение D = b2 − 4ac называют дискриминантом квадратного трехчлена ax2 + bx + c и дискриминантом связанного с ним квадратного уравнения ax2 + bx + c = 0. От знака дискриминанта зависит, пересекает ли график квадратного трехчлена ось абсцисс или лежит по одну сторону от нее. Именно, если D < 0, то парабола не имеет общих точек с осью Ox, при этом: если a > 0, то парабола лежит выше оси Ox, а если a < 0, то ниже этой оси (рис. 4). В случае D > 0 график квадратного трехчлена пересекает ось абсцисс в двух точках x1 и x2, которые являются корнями квадратного уравнения ax2 + bx + c = 0 и равны соответственно
При D = 0 парабола касается оси Ox в точке
x = −b/(2a).
Свойства квадратного трехчлена лежат в основе решения квадратных неравенств. Поясним это на примере. Пусть требуется найти все решения неравенства 3x2 — 2x — 1 < 0. Найдем дискриминант квадратного трехчлена, стоящего в левой части неравенства: D = 16. Так как D > 0, то соответствующее квадратное уравнение 3x2 − 2x − 1 = 0 имеет два различных корня, они определяются по формулам, приведенным ранее:
x1 = −1/3 и x2 = 1.
В рассматриваемом квадратном трехчлене a = 3 > 0, значит, ветви его графика направлены вверх и значения квадратного трехчлена отрицательны лишь в интервале между корнями. Итак, все решения неравенства удовлетворяют условию
−1/3 < x < 1.
К квадратным неравенствам могут быть сведены разнообразные неравенства теми же самыми заменами, какими различные уравнения сводятся к квадратному.
