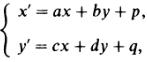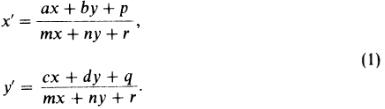Геометрические преобразования

Геометрическое преобразование плоскости — взаимно-однозначное отображение этой плоскости на себя. Наиболее важными геометрическими преобразованиями являются движения, т. е. преобразования, сохраняющие расстояние. Иначе говоря, если f — движение плоскости, то для любых двух точек A, B этой плоскости расстояние между точками f(A) и f(B) равно |AB|.

Движения связаны с понятием равенства (конгруэнтности) фигур: две фигуры F и G плоскости α называются равными, если существует движение этой плоскости, переводящее первую фигуру во вторую. Фактически это определение использовал еще Евклид (см. Геометрия), называвший две фигуры равными, если одну из них можно наложить на другую так, чтобы они совпали всеми своими точками; под наложением здесь следует понимать перекладывание фигуры как твердого целого (без изменения расстояний), т. е. движение.

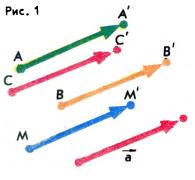
Примерами движений плоскости являются осевая и центральная симметрия, параллельный перенос, поворот. Как пример, напомним определение параллельного переноса. Пусть a^→ — некоторый вектор плоскости α. Геометрическое преобразование, переводящее каждую точку A∈α в такую точку А', что АА'^→ = a^→ (рис. 1), называется параллельным переносом на вектор а^→. Параллельный перенос является движением: если точки А и В переходят в А' и B', т.е. АА'^→ = а^→, ВВ'^→ = а^→, то А'В'^→ = А'А^→ + АВ^→ + ВВ'^→ = -а^→ + АВ^→ + а^→ = АВ^→, и потому |А'В'| = |АВ|.

При решении геометрических задач с помощью движений часто применяется свойство сохранения пересечения: при любом движении f пересечение фигур переходит в пересечение их образов, т. е. если P, Q — произвольные фигуры, то фигура P ⋂ Q переходит в результате движения в фигуру f(P) ⋂ f(Q). (Аналогичное свойство справедливо для объединения.)

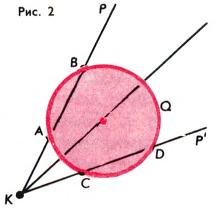
Задача 1. Окружность, центр которой принадлежит биссектрисе угла, пересекает его стороны в точках A, B, C и D (рис. 2). Доказать, что |AB| = |CD|.

Решение. Обозначим через P одну из сторон угла, а через Q — круг, границей которого является рассматриваемая окружность. При симметрии s относительно биссектрисы угла луч P переходит в луч P′, который образует вторую сторону угла, а круг Q переходит в себя: s(P) = P′, s(Q) = Q. Согласно свойству сохранения пересечения фигура P ⋂ Q переходит в s(P) ⋂ s(Q), т. е. в P′ ⋂ Q. Иначе говоря, отрезок AB переходит в отрезок CD, и потому |AB| = |CD|.

Задача 2. Через точку A, данную внутри угла (меньшего, чем развернутый), провести прямую, отрезок которой, заключенный между сторонами угла, делится в этой точке пополам.

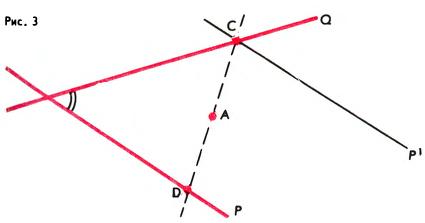
Решение. Обозначим через z симметрию относительно точки A, а через P и Q — прямые, на которых лежат стороны угла (рис. 3). В результате симметрии z прямая P переходит в параллельную ей прямую P′ которая пересекает вторую сторону угла в точке C. Так как C ∈ P′, то точка D, симметричная C, принадлежит прямой, которая симметрична P′, т. е. D ∈ P. Таким образом, точки D ∈ P и C ∈ Q симметричны относительно A, и потому отрезок CD делится в точке A пополам, т. е. прямая CD — искомая.

Нетрудно понять, почему в задаче 1 была применена осевая, а в задаче 2 — центральная симметрия. Так как биссектриса угла — его ось симметрии, то попытка применить осевую симметрию в задаче 1 совершенно естественна (так же, как и применение центральной симметрии в задаче 2, поскольку отрезок CD должен делиться в точке A пополам, т. е. искомые точки C и D должны быть симметричными относительно точки A). И в других случаях анализ условия задачи позволяет найти движение, применение которого дает решение.

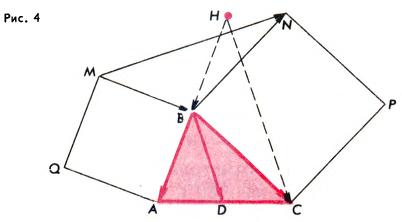
Задача 3. На сторонах AB и BC треугольника ABC построены вне его квадраты ABMQ и BCPN. Доказать, что отрезок MN перпендикулярен медиане BD треугольника ABC и вдвое длиннее этой медианы.

Решение. Попытаемся применить поворот на 90°, т. е. убедиться, что при повороте на 90° вокруг точки B (по часовой стрелке) отрезок MN перейдет в отрезок, параллельный BD и имеющий вдвое большую длину. При этом повороте вектор MB^→ переходит в HB^→ (рис. 4), а вектор BN^→ в BC^→. Следовательно, вектор MN^→ = MB^→ + BN^→ переходит в HB^→ + BC^→, т. е. в HC^→. Но так как HB^→ = BA^→, то HB^→ + BC^→ = BA^→ + BC^→ = 2BD^→. Итак, при повороте на 90° вектор MN^→ переходит в HC^→, т.е. в вектор, равный 2BD^→. Отсюда вытекает, что MN ⊥ BD и |MN| = 2|BD|.

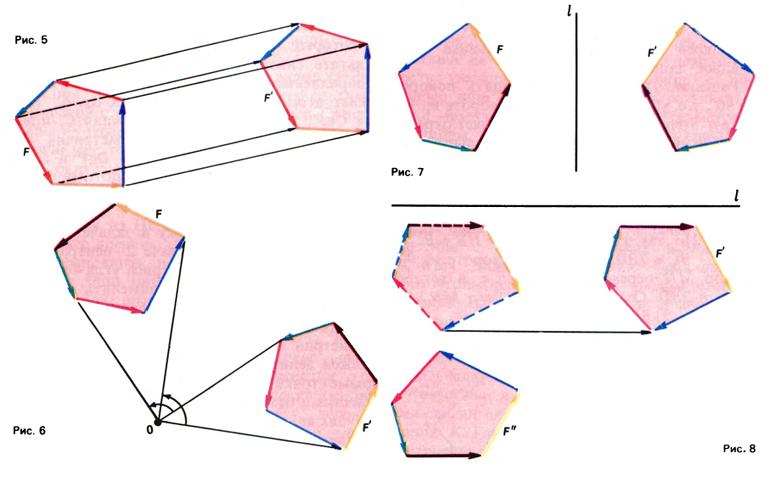
Весьма существенна связь движений с ориентацией. На рис. 5 изображен многоугольник F, на контуре которого задано положительное направление обхода (против часовой стрелки). При параллельном переносе получается многоугольник с тем же направлением обхода, т. е. параллельный перенос сохраняет направление обхода, или, как говорят, сохраняет ориентацию. Поворот (в частности, центральная симметрия, представляющая собой поворот на 180°) также сохраняет ориентацию (рис. 6). Напротив, осевая симметрия меняет направление обхода на противоположное (рис. 7), т. е. меняет ориентацию. Другой пример движения, меняющего ориентацию — скользящая симметрия, т. е. композиция симметрии относительно некоторой прямой l и параллельного переноса, вектор которого параллелен l (рис. 8).

Французский механик и геометр XIX в. М. Шаль сформулировал следующую теорему: всякое сохраняющее ориентацию движение плоскости является либо параллельным переносом, либо поворотом; всякое меняющее ориентацию движение плоскости является либо осевой, либо скользящей симметрией.

Задача 4. Доказать, что композиция двух осевых симметрий с пересекающимися осями представляет собой поворот.

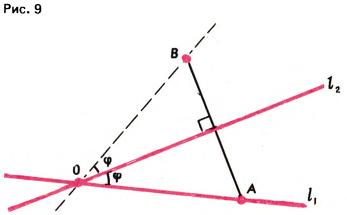
Решение. Пусть s₁ и s₂ — осевые симметрии, оси которых (прямые l₁ и l₂) пересекаются в точке O. Так как оба движения s₁, s₂ меняют ориентацию, то их композиция s₂ ∘ s₁ (сначала выполняется s₁ затем s₂) является движением, сохраняющим ориентацию. По теореме Шаля, s₂ ∘ s₁ есть либо параллельный перенос, либо поворот. Но так как при каждом движении s₁, s₂ точка O неподвижна, то и при их композиции точка O остается на месте. Следовательно, s₂ ∘ s₁ есть поворот вокруг точки O. Как найти угол поворота, понятно из рис. 9: если φ — угол между прямыми l₁ и l₂, то (поскольку точка A ∈ l₁ переводится движением s₁ в себя, а движением s₂ — в симметричную относительно l₂ точку B) движение s₂ ∘ s₁ переводящее A в B, представляет собой поворот (вокруг точки O) на угол 2φ.

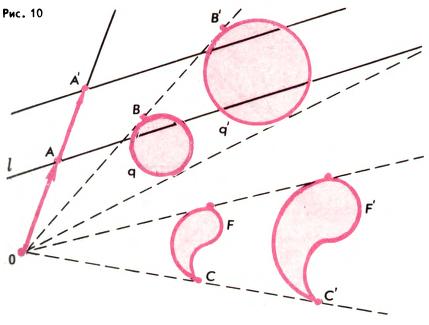
Следующую по важности группу геометрических преобразований плоскости составляют преобразования подобия. Наиболее простое из них — гомотетия. Напомним, что гомотетией с центром O и коэффициентом k ≠ 0 называется геометрическое преобразование, которое произвольно взятую точку A переводит в такую точку A′, что OA′^→ = kOA^→ (рис. 10). Гомотетия переводит каждую прямую в параллельную ей прямую, каждую окружность снова переводит в окружность. Гомотетия сохраняет углы, а все длины увеличивает в |k| раз: если при гомотетии точки A, B переходят в A′B′, то |A′B′| = |k|•|AB|. Из этого вытекает, что гомотетия сохраняет форму (но не размеры) фигур; если, например, k > 1, то фигура F′, в которую переходит фигура F при гомотетии с центром O и коэффициентом k, представляет собой увеличенную копию фигуры F (рис. 10), а если 0 < k < 1 — уменьшенную копию.

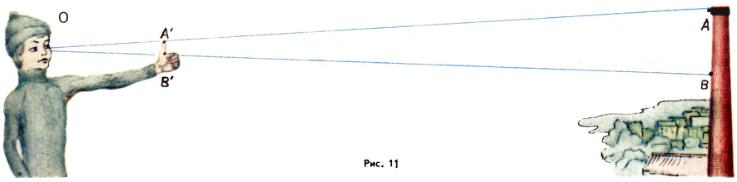
Поскольку при гомотетии все длины изменяются в одинаковое число раз, отношение длин не меняется. На этом основаны различные способы оценки расстояний; например, зная длину руки и длину большого пальца и прикинув, сколько раз большой палец вытянутой руки укладывается в видимом образе предмета, можно найти отношение высоты вертикального предмета к расстоянию до него (на рис. 11 имеем |AB|:|BO| = |A′B′|:|B′O|, откуда, измерив |BO|, можно найти |AB|, а потому и высоту трубы, которая примерно втрое больше |AB|.

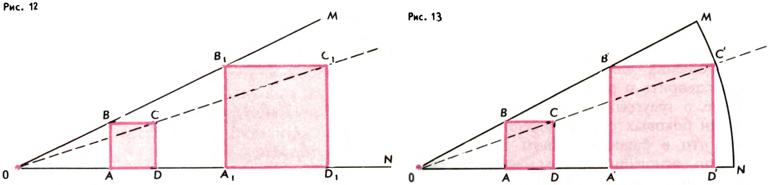
Задача 5. Построить квадрат, вписанный в данный сектор (две вершины квадрата лежат на одном радиусе, третья — на другом, четвертая — на дуге сектора).

Решение. Пусть ABCD и A₁B₁C₁D₁ (рис. 12) — два квадрата, вписанные в угол MON. При гомотетии с центром O, переводящей точку B в B₁ (коэффициент этой гомотетии равен k = |OB₁| / |OB|), отрезок AB переходит в отрезок A₁B₁, а потому квадрат ABCD переходит в квадрат A₁B₁C₁D₁ (поскольку углы, а также отношение отрезков сохраняются). Из этого вытекает, что вершины C и C₁ лежат на одном луче, исходящем из точки O. Теперь ясно, что, построив какой-нибудь квадрат ABCD, вписанный в угол MON, и проведя луч OC, мы сможем найти вершину C′ искомого квадрата (т. е. точку пересечения луча OC с дугой MN сектора), а затем достроить искомый квадрат (рис. 13).

Преобразование f плоскости α называется подобием с коэффициентом k > 0, если для любых точек A, B плоскости α расстояние между точками f(A) и f(B) равно k•|AB|. Любое подобие (как и гомотетия — частный случай подобия) сохраняет углы, а также отношение длин, т. е. сохраняет форму фигур. Однако, в отличие от гомотетии, подобие может переводить прямую l в прямую l′, не параллельную ей.

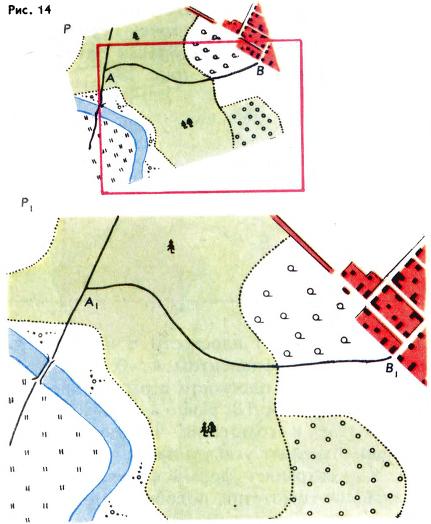
На рис. 14 изображены два плана P и P₁ одного и того же участка местности, выполненные в разных масштабах и по‑разному лежащие на плоскости. Эти планы представляют собой подобные, но не гомотетичные фигуры; например, прямая AB и соответствующая ей прямая A₁B₁ не параллельны. Чтобы получить план P₁ исходя из плана P, можно поступить так: сначала повернуть план P, чтобы его стороны стали параллельными сторонам плана P₁, а затем применить гомотетию. Иначе говоря, план P₁, подобный P, получается из P при помощи композиции движения (поворота) и гомотетии.

Указанное обстоятельство является общим, т. е. всякое подобие g представляется в виде композиции h ∘ f, где f — движение, а h — гомотетия. Из этого ясно, что при решении задач методом подобия можно ограничиваться лишь рассмотрением гомотетии (сопровождаемой некоторым движением). Это имеет определенные удобства: вспомните, с каким напряженным вниманием отыскиваются соответственные стороны по‑разному расположенных подобных треугольников при выписывании равенства отношений сторон (и с какой легкостью выписываются эти отношения для гомотетичных треугольников).

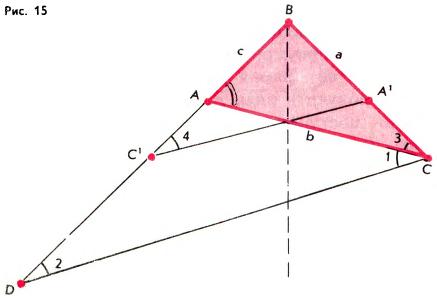
Задача 6. Стороны треугольника ABC связаны соотношением a² = c(b + c). Доказать, что угол A вдвое больше угла C.

Решение. Пусть D — такая точка прямой AB, что |AD| = b, причем A лежит между B и D (рис. 15). Тогда треугольник ACD — равнобедренный, и потому ∠1 = ∠2; кроме того, |BD| = b + c. При симметрии относительно биссектрисы угла B точки A и C перейдут в такие точки A′ и C′, что |BA′| = |BA| = c, |BC′| = |BC| = a; кроме того ∠3 = ∠4. Равенство a² = c(b + c) можно переписать в виде

(b + c)/a = a/c, т. е |BD| / |BC| = |BC′| / |BA′|,

откуда следует, что при гомотетии с центром B и коэффициентом k = |BD| / |BC′| точки D, C переходят в C′, A′. Следовательно, DC || C′A′ и потому ∠2 = ∠4, т. е. ∠1 = ∠2 = ∠3 = ∠4. Так как BAC — внешний угол треугольника ACD, то он равен сумме углов ∠1 и ∠2, т. е. равен удвоенному углу C.

В заключение рассказа о преобразованиях подобия заметим, что они составляют группу преобразований и потому (см. Геометрия) согласно Эрлангенской программе определяют «свою» геометрию. Инвариантами этой группы (т. е. теми свойствами, которые сохраняются при всех преобразованиях подобия и изучаются в геометрии подобий) являются угол, отношение длин двух отрезков, параллельность двух прямых и т. д. Хотя длина отрезка уже не сохраняется, но в силу сохранения отношения длин в геометрии подобий можно говорить о равнобедренном треугольнике (т. е. о треугольнике, в котором отношение длин боковых сторон равно 1). Теорема о том, что в равнобедренном треугольнике углы при основании равны, сохраняется и в геометрии подобий. Сохраняется также теорема Пифагора (в форме (a/c)² + (b/c)² = 1, где a/c и b/c — отношения длин катетов к длине гипотенузы) и т. п.

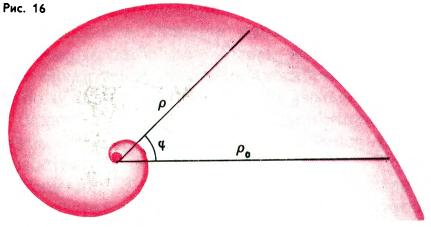
Однако не следует думать, что геометрия подобий ничем, кроме формы изложения, не отличается от евклидовой геометрии. Существуют факты, которые отличают эти две геометрии. Например, условимся говорить, что линия L может скользить по себе, если для любых двух точек A, B этой линии найдется преобразование f (принадлежащее группе, задающей рассматриваемую геометрию), которое переводит линию L в себя, а точку A — в B. В геометрии Евклида (т. е. в геометрии, определяемой группой движений плоскости) существуют только два типа связных линий (т. е. состоящих из одного куска), которые могут скользить по себе: прямые и окружности. А в геометрии подобий существуют линии, отличные от прямых и окружностей, которые могут скользить по себе; это — логарифмические спирали, определяемые в полярных координатах уравнением ρ = ρ₀e^kφ (рис. 16).

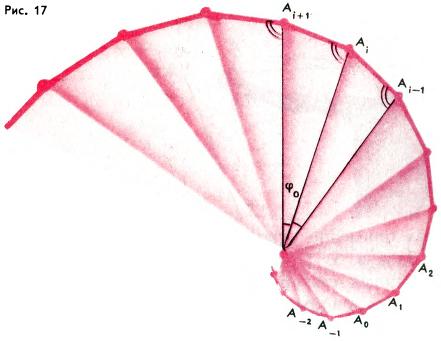
Еще один необычный факт геометрии подобий мы получим, рассматривая преобразование g = h ∘ r, где r — поворот вокруг точки O на угол φ₀, а h — гомотетия с центром O и коэффициентом k₀ > 0. Пусть …, A₋₂, A₋₁, A₀, A₁, A₂, … — последовательность точек, переходящих друг в друга при преобразовании g, т. е. g(A_i) = A_i+1 при любом целом i (рис. 17). Эти точки лежат на одной логарифмической спирали, причем для любого целого i угол A_iOA_i+1 имеет одну и ту же величину φ₀. Последовательно соединяя эти точки, мы получим бесконечную ломаную линию …A₋₂A₋₁A₀A₁A₂…, которая переводится преобразованием g в себя, причем каждая вершина A_i переводится в соседнюю вершину A_i+1.

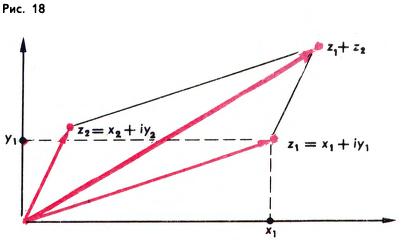
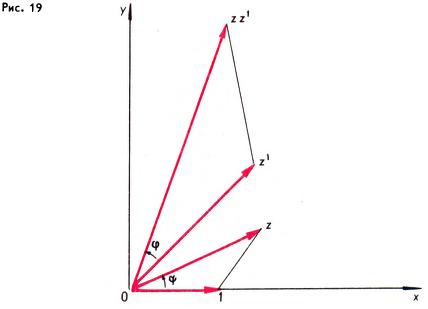
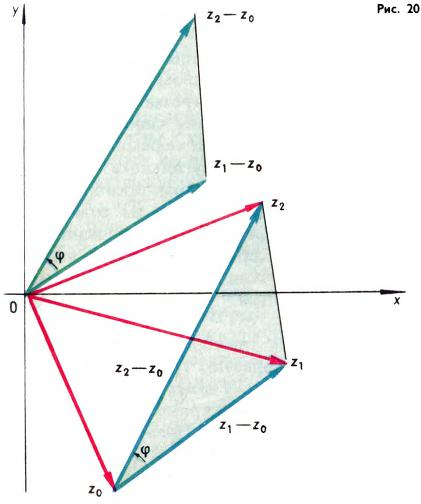
Заметим, что рассмотренное преобразование подобия g = h ∘ r (его называют поворотным растяжением) имеет тесную связь с комплексными числами. Комплексное число z = x + iy можно представить в виде направленного отрезка, идущего из начала координат в точку (x; y). При таком геометрическом изображении комплексные числа складываются как векторы (рис. 18). А для получения геометрической интерпретации умножения комплексных чисел удобно поворотное растяжение g = h ∘ r, рассмотренное выше. Именно, пусть z = x + iy — некоторое комплексное число, ρ — его модуль (т. е. длина изображающего отрезка), а φ — аргумент (т. е. угол наклона изображающего направленного отрезка к положительной части оси абсцисс). Число z получается из числа 1, если, во‑первых, вектор, изображающий число 1, растянуть в ρ раз, и, во‑вторых, повернуть его на угол φ (рис. 19), т. е. вектор z получается из вектора 1 преобразованием g = h ∘ r = r ∘ h, где h — гомотетия с центром в начале и коэффициентом ρ, а r — поворот вокруг начала на угол φ. Итак, z = g(1). Если теперь z′ = x′ + iy′ — другое комплексное число, то при применении преобразования g (т. е. при растяжении изображающего вектора в ρ раз и повороте его на угол φ) число z′ переходит в zz′ (рис. 19). Можно сказать и иначе: треугольники на рис. 19 подобны. Это и дает геометрическую интерпретацию умножения комплексных чисел. Из сказанного ясно, что при умножении всех комплексных чисел на одно и то же комплексное число z вся плоскость комплексных чисел подвергается поворотному растяжению. В частности, для любых трех комплексных чисел z₀, z₁, z₂ мы имеем z₂ − z₀ = z(z₁ − z₀), где z — комплексное число, модуль которого равен отношению длин векторов z₂ − z₀ и Z₁ − z₀, а аргумент равен углу между этими векторами (рис. 20).

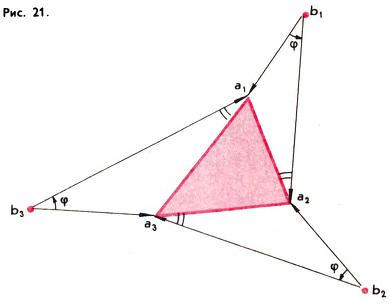
Задача 7. На сторонах треугольника A₁A₂A₃ построены вне его подобные между собой треугольники A₁B₂A₂, A₂B₂A₃, A₃B₃A₁. Доказать, что точка пересечения медиан ∆B₁B₂B₃ совпадает с точкой пересечения медиан ∆A₁A₂A₃.

Решение. Обозначим через a₁, a₂, a₃, b₁, b₂, b₃ комплексные числа, изображаемые векторами OA₁^→, OA₂^→, OA₃^→, OB₁^→, OB₂^→, OB₃^→. Тогда a₂ − b₁ = z(a₁ − b₁), a₃ − b₂ = z(a₂ − b₂), a₁ − b₃ = z (a₃ − b₃), где z — комплексное число, модуль которого равен отношению боковых сторон рассматриваемых подобных треугольников, а аргумент равен φ (рис. 21). Складывая эти равенства, получаем (после очевидных упрощений):

(z − 1)(b₁ + b₂ + b₃) = (z − 1)(a₁ + a₂ + a₃).

Так как z ≠ 1 (поскольку аргумент φ числа z отличен от нуля), то отсюда следует, что b₁ + b₂ + b₃ = a₁ + a₂ + a₃. Переходя к векторным обозначениям и деля на 3, получаем

1/3 (OB₁^→ + OB₂^→ + OB₃^→) = 1/3 (OA₁^→ + OA₂^→ + OA₃^→),

а это и означает, что точки пересечения медиан ∆B₁B₂B₃ и ∆A₁A₂A₃ совпадают (см. Вектор).

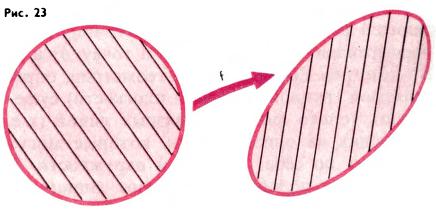
Расскажем коротко и о других преобразованиях, играющих важную роль в современной геометрии. Преобразование f евклидовой плоскости называется аффинным, если оно каждую прямую переводит снова в прямую, а параллельные между собой прямые — снова в параллельные (рис. 22). Если на плоскости введена система координат, то аффинное преобразование задается линейными соотношениями, т. е. точка A′(x′; y′), в которую переходит точка A(x; y), определяется формулами

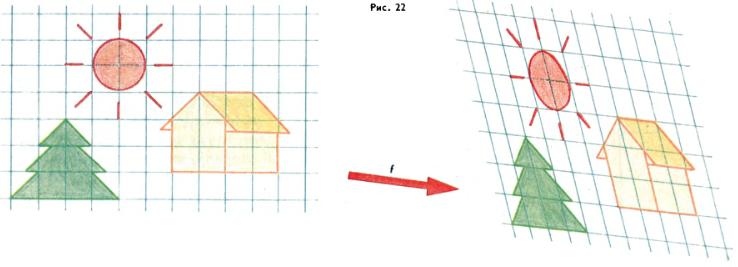
где ad − bc ≠ 0 (и обратно: такими формулами задается некоторое аффинное преобразование). Далее, если A, B, C — три точки плоскости, не лежащие на одной прямой, и A′, B′, C′ — три другие точки, также не лежащие на одной прямой, то существует, и притом только одно, аффинное преобразование, переводящее точки A, B, C соответственно в A′, B′, C′. Отметим, что длины и углы могут изменяться при аффинных преобразованиях. Не сохраняется (в отличие от преобразований подобия) и отношение длин отрезков. Однако отношение длин двух параллельных отрезков сохраняется при любом аффинном преобразовании. В частности, середина отрезка переходит при аффинном преобразовании снова в середину отрезка, параллелограмм переходит в параллелограмм, медиана треугольника в медиану и т. п. Круг при аффинном преобразовании переходит в эллипс, причем из отмеченных выше свойств аффинных преобразований легко следует, что середины параллельных между собой хорд эллипса лежат на одном отрезке, проходящем через центр эллипса (рис. 23).

Все аффинные преобразования плоскости, вместе взятые, образуют группу преобразований, и потому (см. Геометрия) они определяют некоторую геометрию. Она называется аффинной геометрией. Инвариантами этой группы (т. е. теми свойствами фигур, которые изучаются в аффинной геометрии) являются прямолинейное расположение точек, параллельность, отношение длин параллельных отрезков и другие свойства, получаемые из этих (например, наличие у фигуры центра симметрии). Не говоря более подробно об этой геометрии, покажем на примерах, как отмеченные выше свойства аффинных преобразований могут быть применены при решении задач.

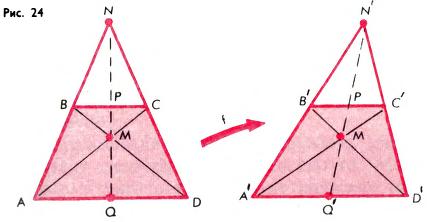
Задача 8. Доказать, что в произвольной трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.

Решение. Для равнобочной трапеции это очевидно (так как равнобочная трапеция симметрична относительной прямой, проходящей через середины оснований). Пусть теперь A′B′C′D′ — произвольная трапеция и пусть ABCD — равнобочная трапеция с теми же длинами оснований (рис. 24). Рассмотрим аффинное преобразование, переводящее точки A, B, C соответственно в A′, B′, C′. При этом преобразовании прямые AD, BC перейдут в A′D′, B′C′ (поскольку AD ∥ BC, а параллельность прямых сохраняется). Далее, так как |AD| / |BC| = |A′D′| / |B′C′|, то точка D перейдет в D′ (поскольку отношение параллельных отрезков сохраняется). Иначе говоря, трапеция ABCD перейдет в трапецию A′B′C′D′. Следовательно, прямолинейное расположение точек N, P, Q сохранится, т. е. в трапеции A′B′C′D′ точки M′, N′, P′, Q' также лежат на одной прямой.

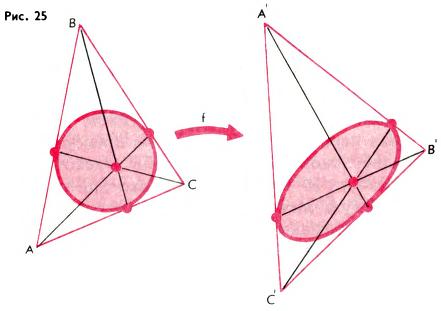
Задача 9. В треугольнике A′B′C′ вписан эллипс и проведены три отрезка, каждый из которых соединяет вершину и точку касания эллипса с противоположной стороной. Доказать, что эти три отрезка пересекаются в одной точке.

Решение. Пусть f — аффинное преобразование, которое переводит некоторую окружность в рассматриваемый эллипс, и пусть ABC — треугольник, который при этом преобразовании переходит в ∆A′B′C′. Так как для вписанной окружности рассматриваемое свойство, как нетрудно доказать, справедливо (левая часть рис. 25), то оно справедливо и для вписанного эллипса (правая часть рисунка).

В статье «Проективная геометрия» рассказано о том, как пополнение плоскости несобственными («бесконечно удаленными») точками превращает её в проективную плоскость. Геометрические преобразования проективной плоскости, которые сохраняют прямолинейное расположение точек, называются проективными преобразованиями. Проективные преобразования задаются в координатах дробно-линейными формулами:

Более подробно: если π — евклидова плоскость, в которой задана система координат, а π* — проективная плоскость, получающаяся из π присоединением несобственных элементов, то любое проективное преобразование плоскости π* записывается в рассматриваемых координатах формулами (1) при условии, что точка A(x; y) и точка A′(x′; y′) в которую она переходит, не являются несобственными.

Проективные преобразования образуют группу преобразований проективной плоскости. Согласно Эрлангенской программе, эта группа определяет некоторую геометрию — это и есть проективная геометрия. Инвариантами проективных преобразований (т. е. теми свойствами фигур, которые изучаются в проективной геометрии) являются прямолинейное расположение точек, ангармоническое отношение четырех точек, лежащих на одной прямой, и др.

Если A, B, C, D — четыре точки проективной плоскости, никакие три из которых не лежат на одной прямой, и A′, B′, C′, D′ — другие четыре точки этой плоскости, из которых также никакие три не лежат на одной прямой, то существует, и притом только одно, проективное преобразование, которое переводит A, B, C, D соответственно в A′, B′, C′, D′. Пользуясь перечисленными свойствами проективных преобразований, можно решать различные геометрические задачи.

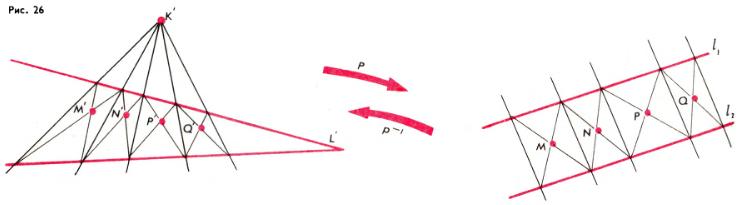
Задача 10. Доказать, что точки M′, N′, P′, Q′ на рис. 26 лежат на одной прямой.

Решение. Пусть p — проективное преобразование, переводящее K′ и L′ в несобственные точки; мы получим (в евклидовой плоскости) расположение точек, показанное на рис. 26 справа. В этом случае точки M, N, P, Q, очевидно, лежат на одной прямой (на средней линии полосы между прямыми l₁ и l₂). Применяя обратное преобразование p⁻¹ мы заключаем, что и на рис. 26 слева точки M′, N′, P′, Q′ лежат на одной прямой (поскольку при проективном преобразовании p⁻¹ сохраняется прямолинейное расположение точек).

Все рассмотренные выше преобразования сохраняли прямолинейное расположение точек (на евклидовой или на проективной плоскости). Иначе говоря, система всех прямых линий на плоскости переводится снова в эту же систему линий. Существует интересный класс преобразований, который обладает аналогичным свойством по отношению к другой системе линий. Именно: рассмотрим на плоскости (евклидовой) систему, состоящую из всех прямых линий и всех окружностей. Преобразования, которые эту систему линий переводят снова в эту же систему, называются круговыми преобразованиями. Иначе говоря, прямая переходит при круговом преобразовании либо снова в прямую, либо в некоторую окружность (и то же справедливо для окружности). Чуть ниже мы уточним одно соглашение относительно евклидовой плоскости, которое требуется при рассмотрении круговых преобразований, но вначале рассмотрим один важный пример кругового преобразования — так называемую инверсию.

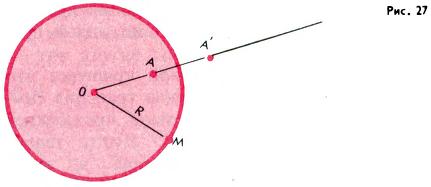
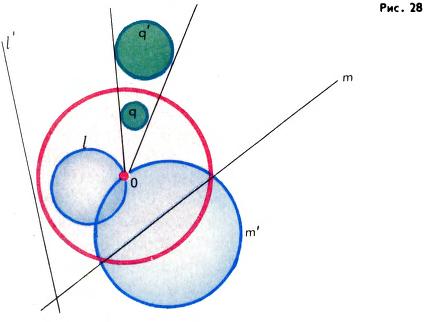
Пусть задана некоторая точка O плоскости и некоторое положительное число R. Геометрическое преобразование, которое каждую отличную от O точку A плоскости переводит в такую точку A′ луча OA, что |OA| • |OA'| = R², называется инверсией с центром O и радиусом R (рис. 27). Название «радиус» инверсии объясняется тем, что каждая точка окружности с центром O и радиусом R, очевидно, остается неподвижной при этом преобразовании (т. е. переходит в себя). Точки, лежащие внутри этой окружности (называемой окружностью инверсии), переходят в точки, лежащие вне её, и наоборот. На этом основании инверсию часто называют симметрией относительно окружности. Инверсия является круговым преобразованием: каждая прямая или окружность переходит снова в прямую или окружность (рис. 28). Заметим теперь, что точка O (центр инверсии) не имеет образа при этом преобразовании, но если точка A приближается к O (не совпадая с ней), то соответствующая точка A′ неограниченно удаляется от O. На этом основании условились считать, что на плоскости существует одна несобственная точка ∞, и при инверсии с центром O точка O переходит в ∞, а ∞ переходит в O. Плоскость, пополненная точкой ∞, называется круговой плоскостью (в отличие от проективной плоскости, которая получается присоединением не одной, а бесконечно многих несобственных точек). Теперь инверсия становится взаимно-однозначным преобразованием плоскости (круговой).

Помимо того что инверсия переводит систему всех прямых и окружностей снова в эту же систему, инверсия обладает еще рядом замечательных свойств, делающих её важным инструментом при решении ряда геометрических задач. Основным из них является то, что инверсия сохраняет углы: если две линии l и m пересекаются под углом φ (т. е. угол между касательными к этим линиям в их общей точке равен φ), то образы l′ и m′ этих линий пересекаются под тем же углом φ. Если, в частности, окружность l ортогональна окружности инверсии, т. е. пересекает её под прямым углом (о таких окружностях шла речь в конце статьи Геометрия Лобачевского), то при инверсии эта окружность l переходит в себя (только части её, лежащие внутри и вне окружности инверсии, меняются местами). Инверсия является важнейшим из круговых преобразований: можно доказать, что любое круговое преобразование плоскости является либо инверсией, либо подобием, либо композицией инверсии и подобия. Вместе взятые, круговые преобразования составляют группу преобразований, которая определяет на круговой плоскости своеобразную геометрию («круговую»).

Мы рассказали о наиболее важных геометрических преобразованиях плоскости. Можно рассматривать также геометрические преобразования трехмерного пространства, плоскости (или пространства) Лобачевского и других геометрических объектов. Заметим, в частности, что если f — движение трехмерного пространства R³, переводящее плоскость α ⊂ R³ в некоторую плоскость β, а p — центральное проектирование плоскости β на α из некоторой точки O (не принадлежащей плоскостям α и β), то композиция p ∘ f представляет собой проективное преобразование плоскости α (поскольку и f, и p переводят прямую снова в прямую). Оказывается, что в таком виде можно представить любое проективное преобразование плоскости α.

Знакомство с геометрическими преобразованиями и умение применять их является важным элементом математической культуры.