Вектор

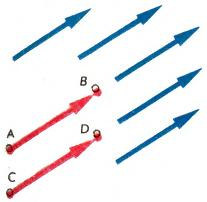
Вектор — одно из основных геометрических понятий. Вектор характеризуется числом (длиной) и направлением. Наглядно его можно представить себе в виде направленного отрезка, хотя, говоря о векторе, правильнее иметь в виду целый класс направленных отрезков, которые все параллельны между собой, имеют одинаковую длину и одинаковое направление (рис. 1). Примерами физических величин, которые имеют векторный характер, могут служить скорость (поступательно движущегося тела), ускорение, сила и др.

Понятие вектора появилось в работах немецкого математика XIX в. Г. Грассмана и ирландского математика У. Гамильтона; затем оно было охотно воспринято многими математиками и физиками. В современной математике и её приложениях это понятие играет важнейшую роль. Векторы применяются в классической механике Галилея-Ньютона (в её современном изложении), в теории относительности, квантовой физике, в математической экономике и многих других разделах естествознания, не говоря уже о применении векторов в различных областях математики.

• 

  Рис 1.

• 

  Рис 2.

• 

  Рис 3.

• 

  Рис 4.

• 

  Рис 5.

• 

  Рис 6.

• 

  Рис 7.

Каждый из направленных отрезков, составляющих вектор (рис. 1), можно назвать представителем этого вектора. Вектор, представителем которого является направленный отрезок, идущий от точки [math]A[/math] к точке [math]B[/math], обозначается через [math]\overrightarrow{AB}.[/math] На рис. 1 имеем [math]\overrightarrow{AB}=\overrightarrow{CD},[/math] т. е. [math]\overrightarrow{AB}[/math] и [math]\overrightarrow{CD}[/math] — это один и тот же вектор (представителями которого являются оба направленных отрезка, выделенных на рис. 1). Иногда вектор обозначают малой буквой со стрелкой: [math]\overrightarrow{a},\ \overrightarrow{b}.[/math]

Вектор, изображаемый направленным «отрезком», у которого начало и конец совпадают, называется нулевым; он обозначается через [math]\overrightarrow{0},[/math] т. е. [math]\overrightarrow{AA}=\overrightarrow{0}.[/math]. Два параллельных вектора, имеющих одинаковые длины, но противоположные направления, называются противоположными. Если вектор обозначен через [math]\overrightarrow{a},[/math] то противоположный ему вектор обозначается через [math]−\overrightarrow{a}.[/math]

Назовем основные операции, связанные с векторами.

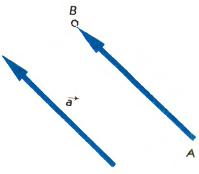
[math]\text{I}.[/math] Откладывание вектора от точки. Пусть [math]\overrightarrow{a}[/math] — некоторый вектор и [math]A[/math] — точка. Среди направленных отрезков, являющихся представителями вектора [math]\overrightarrow{a},[/math] имеется направленный отрезок, начинающийся в точке [math]A.[/math] Конец [math]B[/math] этого направленного отрезка называется точкой, получающейся в результате откладывания вектора [math]\overrightarrow{a}[/math] от точки [math]A[/math] (рис. 2). Эта операция обладает следующим свойством:

[math]{{\text{I}}_{1}}.[/math] Для любой точки [math]A[/math] и любого вектора [math]\overrightarrow{a}[/math] существует, и притом только одна, точка [math]B,[/math] для которой [math]\overrightarrow{AB}=\overrightarrow{a}.[/math]

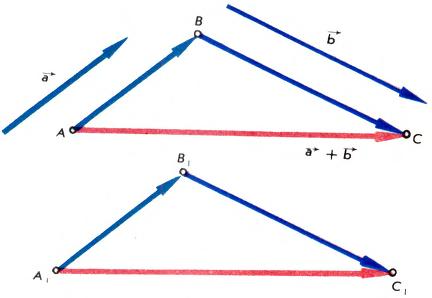
Сложение векторов. Пусть [math]\overrightarrow{a}[/math] и [math]\overrightarrow{b}[/math] - два вектора. Возьмем произвольную точку [math]A[/math] и отложим вектор [math]\overrightarrow{a}[/math] от точки [math]A,[/math] т. е. найдем такую точку [math]B,[/math] что [math]\overrightarrow{AB}=\overrightarrow{a}[/math] (рис. 3). Затем от точки [math]B[/math] отложим вектор [math]\overrightarrow{b},[/math] т. е. найдем такую точку [math]C,[/math] что [math]\overrightarrow{BC}=\overrightarrow{b}.[/math] Вектор [math]\overrightarrow{AC}[/math] называется суммой векторов [math]\overrightarrow{a}[/math] и [math]\overrightarrow{b}[/math] и обозначается через [math]\overrightarrow{a}+\overrightarrow{b}.[/math] Можно доказать, что сумма [math]\overrightarrow{a}+\overrightarrow{b}\lt /math не зависит от выбора точки \lt math\gt A[/math], т. е. если заменить [math]A[/math] другой точкой [math]{{A}_{1}},[/math] то получится вектор [math]\overrightarrow{{{A}_{1}}{{C}_{1}}},[/math] равный [math]\overrightarrow{AC}[/math] (рис. 3). Из определения суммы векторов вытекает, что для любых трех точек [math]A,B,C[/math] справедливо равенство

[math]{{\text{I}}_{2}}:[/math] [math]\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}[/math]

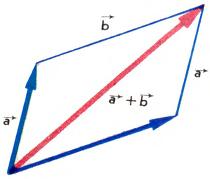
(«правило трех точек»). Если ненулевые векторы [math]\overrightarrow{a}[/math] и [math]\overrightarrow{b}[/math] не параллельны, то их сумму удобно находить с помощью правила параллелограмма (рис. 4).

[math]\text{II}.[/math] Основные свойства суммы векторов выражают следующие 4 равенства (справедливые для любых векторов [math]\overrightarrow{a},[/math] [math]\overrightarrow{b,}[/math] [math]\overrightarrow{c}[/math]):

[math]{{\text{II}}_{1}}.[/math] [math]\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}.[/math]

[math]{{\text{II}}_{2}}.[/math] [math]\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})=(\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}.[/math]

[math]{{\text{II}}_{3}}.[/math] [math]\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}.[/math]

[math]{{\text{II}}_{4}}.[/math] [math]\overrightarrow{a}+(−\overrightarrow{a})=\overrightarrow{0}.[/math]

Заметим еще, что сумма нескольких векторов находится последовательным нахождением суммы двух из них. Например:

[math]\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}=((\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c})+\overrightarrow{d}.[/math]

При этом, в каком бы порядке мы ни складывали заданные векторы, результат (как это вытекает из свойств, названных в пунктах [math]{{\text{II}}_{1}}[/math] и [math]{{\text{II}}_{2}}[/math] всегда будет одним и тем же. Например:

[math]\overrightarrow{a}+((\overrightarrow{b}+\overrightarrow{c})+\overrightarrow{d})=(\overrightarrow{d}+\overrightarrow{a})+(\overrightarrow{c}+\overrightarrow{b}).[/math]

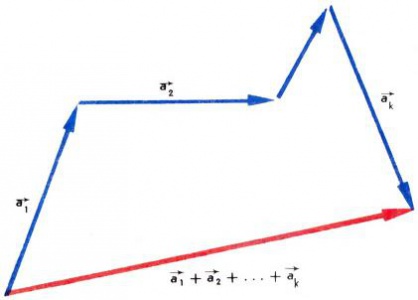
Далее, геометрически сумма нескольких векторов [math]\overrightarrow{{{a}_{1}}},\overrightarrow{{{a}_{1}}}\ …\ \overrightarrow{{{a}_{k}}}[/math] может быть получена следующим образом: надо направленные отрезки, являющиеся представителями этих векторов, последовательно отложить друг за другом (т.е. так, чтобы начало второго направленного отрезка совпадало с концом первого, начало третьего - с концом второго и т.д.); тогда вектор [math]\overrightarrow{{{a}_{1}}}+\overrightarrow{{{a}_{1}}}+…+\overrightarrow{{{a}_{k}}}[/math] будет иметь своим представителем «замыкающий» направленный отрезок, идущий от начала первого к концу последнего (рис. 5). (Заметим, что если при таком последовательном откладывании получается «замкнутая векторная ломаная», то [math]\overrightarrow{{{a}_{1}}}+\overrightarrow{{{a}_{1}}}+…+\overrightarrow{{{a}_{k}}}=0.[/math])

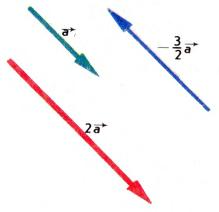
[math]\text{III}.[/math] Умножение вектора на число. Пусть [math]\overrightarrow{a}[/math] — ненулевой вектор и [math]k[/math] — отличное от нуля число. Через [math]k\overrightarrow{a}[/math] обозначается вектор, определяемый следующими двумя условиями: а) длина вектора [math]k\overrightarrow{a}[/math] равна [math]|k||\overrightarrow{a}|[/math] б) вектор [math]k\overrightarrow{a}[/math] параллелен вектору [math]\overrightarrow{a},[/math] причем его направление совпадает с направлением вектора [math]\overrightarrow{a}[/math] при [math]k\gt 0[/math] и противоположно ему при [math]k\lt 0[/math] (рис. б). Если справедливо хотя бы одно из равенств [math]\overrightarrow{a}=\overrightarrow{0},[/math] [math]k=0,[/math] то произведение [math]k\overrightarrow{a}[/math] считается равным [math]\overrightarrow{0}.[/math] Таким образом, произведение [math]k\overrightarrow{a}[/math] определено для любого вектора [math]\overrightarrow{a}[/math] и любого числа [math]k.[/math]

Следующие 4 равенства (справедливые для любых векторов [math]\overrightarrow{a},\overrightarrow{b}[/math] и любых чисел [math]k,l[/math]) выражают основные свойства операции умножения вектора на число:

[math]{{\text{III}}_{1}}.[/math] [math]k(l\overrightarrow{a})=(kl)\overrightarrow{a}.[/math]

[math]{{\text{III}}_{2}}.[/math] [math](k+l)\overrightarrow{a}=k\overrightarrow{a}+l\overrightarrow{a}.[/math]

[math]{{\text{III}}_{3}}.[/math] [math]k(\vec{a}+\overrightarrow{b})=k\vec{a}+k\overrightarrow{b}.[/math]

[math]{{\text{III}}_{4}}.[/math] [math]1\vec{a}=\vec{a}.[/math]

Из этих свойств вытекает ряд дальнейших фактов, связанных с рассмотренными операциями над векторами. Отметим некоторые из них, часто применяемые при решении задач.

а) Если [math]M[/math] — такая точка отрезка [math]AB,[/math] что [math]|AM|:|BM|=k,[/math] то для любой точки [math]O[/math] справедливо равенство [math]\overrightarrow{OM}=(\overrightarrow{OA}+k\overrightarrow{OB})/(k+1),[/math] в частности если [math]M[/math] — середина отрезка [math]AB,[/math] то [math]\overrightarrow{OM}=(\overrightarrow{OA}+\overrightarrow{OB})/2.[/math]

б) Если [math]M[/math] — точка пересечения медиан треугольника [math]ABC,[/math] то [math]\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0};[/math] кроме того, для любой точки [math]O[/math] справедливо равенство [math]\overrightarrow{OM}=(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})/3[/math] (обратные теоремы также справедливы).

в) Пусть [math]M[/math] — точка прямой [math]l[/math] и [math]\overrightarrow{a}[/math] — ненулевой вектор, параллельный этой прямой. Точка [math]A[/math] в том и только в том случае принадлежит прямой [math]l,[/math] если [math]\overrightarrow{MA}=k\vec{a}[/math] (где [math]k[/math] — некоторое число).

г) Пусть [math]M[/math] — точка плоскости [math]α[/math] и [math]\overrightarrow{a},\overrightarrow{b}[/math] — ненулевые и непараллельные между собой векторы, параллельные этой плоскости. Точка [math]A[/math] в том и только в том случае принадлежит плоскости [math]α,[/math] если вектор [math]\overrightarrow{MA}[/math] выражается через [math]\overrightarrow{a}[/math] и [math]\overrightarrow{b},[/math] т. е. [math]\overrightarrow{MA}=k\vec{a}+l\vec{b}.[/math]

Наконец, отметим еще свойство размерности, выражающее тот факт, что пространство трехмерно.

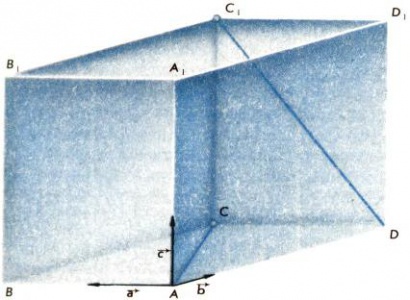
[math]\text{IV}.[/math] В пространстве существуют такие три вектора [math]\overrightarrow{a},\overrightarrow{b},\overrightarrow{c},[/math] что ни один из них не выражается через два других; любой четвертый вектор [math]\overrightarrow{p}[/math] выражается через эти три вектора: [math]\overrightarrow{p}=k\overrightarrow{a}+l\overrightarrow{b}+m\overrightarrow{c}.[/math]

Например, [math]\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}[/math] — три ненулевых вектора, направленных вдоль ребер параллелепипеда, исходящих из одной вершины, то эти векторы [math]\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}[/math] обладают свойством [math]\text{IV}.[/math] (рис. 7).

[math]\text{V}.[/math] Скалярное произведение [math](\overrightarrow{a},\overrightarrow{b})[/math] векторов a^→ и b^→ определяется равенством:

[math](\overrightarrow{a},\overrightarrow{b})=|\overrightarrow{a}||\overrightarrow{b}|\cosφ[/math] при [math]\overrightarrow{a}≠\overrightarrow{0}[/math] и [math]\overrightarrow{b}≠\overrightarrow{0}[/math] где φ - угол между векторами [math]\overrightarrow{a}[/math] и [math]\overrightarrow{b};[/math]

[math](\overrightarrow{a},\overrightarrow{b})=0,[/math] если хотя бы один из векторов [math]\overrightarrow{a},\overrightarrow{b}[/math] равен [math]\overrightarrow{0}.[/math]

Следующие 4 соотношения (справедливые для любых векторов a^→, b^→, c^→ и любого числа k) выражают основные свойства операции скалярного умножения векторов:

[math]{{\text{V}}_{1}}.[/math] [math](\overrightarrow{a},\overrightarrow{b})=(\overrightarrow{b},\overrightarrow{a}).[/math]

[math]{{\text{V}}_{2}}.[/math] [math](k\overrightarrow{a},\overrightarrow{b})=k(\overrightarrow{b},\overrightarrow{a}).[/math]

[math]{{\text{V}}_{3}}.[/math] [math](\overrightarrow{a},\overrightarrow{b}+\overrightarrow{c})=(\overrightarrow{a},\overrightarrow{b})+(\overrightarrow{a},\overrightarrow{c}).[/math]

[math]{{\text{V}}_{4}}.[/math] Если [math]\overrightarrow{a}≠0,[/math] то [math]{{\overrightarrow{a}}^{2}}\gt 0[/math] (здесь через [math]{{\overrightarrow{a}}^{2}}[/math] обозначено скалярное произведение вектора [math]\overrightarrow{a}[/math] на себя).

Заметим в связи со свойством [math]{{\text{V}}_{4}},[/math] что число [math]{{\overrightarrow{a}}^{2}}[/math] равно квадрату длины вектора [math]\overrightarrow{a},[/math] т. е. [math]{{\overrightarrow{a}}^{2}}=|\overrightarrow{a}{{|}^{2}}.[/math]

<addc>G</addc>

Со скалярным произведением связано понятие ортогональности: два вектора [math]\overrightarrow{a}[/math] и [math]\overrightarrow{b}[/math] называются ортогональными, если [math](\overrightarrow{a},\overrightarrow{b})=0.[/math] Иначе говоря, если векторы [math]\overrightarrow{a}[/math] и [math]\overrightarrow{b}[/math] ортогональны, то либо они оба ненулевые и образуют прямой угол, либо хотя бы один из этих векторов равен [math]\overrightarrow{0}[/math] (и тогда угол между ними не определяется).

Перечисленные выше свойства векторных операций во многом похожи на свойства сложения и умножения чисел. В то же время вектор геометрический объект, и в определении векторных операций используются такие геометрические понятия, как длина и угол; этим и объясняется польза векторов для геометрии (и её приложений к физике и другим областям знания). Однако для решения геометрических задач с помощью векторов необходимо прежде всего научиться «переводить» условие геометрической задачи на векторный «язык». После такого «перевода» осуществляются алгебраические вычисления с векторами, а затем полученное векторное решение снова «переводится» на геометрический «язык». В этом и состоит векторное решение геометрических задач.

При изложении курса геометрии в школе вектор дается как определяемое понятие (см. Определение), и потому принятая в школьном учебнике аксиоматика (см. Аксиоматика и аксиоматический метод) геометрии ничего не говорит о свойствах векторов, т. е. все эти свойства должны доказываться как теоремы. Существует, однако, и другой путь изложения геометрии, при котором первоначальными (неопределяемыми) понятиями считаются вектор и точка, а отмеченные выше свойства [math]{{\text{I}}_{1}},[/math] [math]{{\text{I}}_{2}},[/math] [math]{{\text{II}}_{1}—{\text{II}}_{4}},[/math] [math]{{\text{III}}_{1}—{\text{III}}_{4}},[/math] [math]\text{IV},[/math] [math]{{\text{V}}_{1}—{\text{V}}_{4}}[/math] принимаются за аксиомы. Такой путь построения геометрии был предложен в 1917 г. немецким математиком Г. Вейлем. Здесь прямые и плоскости являются определяемыми понятиями. Преимущество такого построения в его краткости и в органической связи с современным пониманием геометрии как в самой математике, так и в других областях знания. В частности, аксиомы [math]{{\text{II}}_{1}—{\text{II}}_{4}},[/math] [math]{{\text{III}}_{1}—{\text{III}}_{4}}[/math] вводят так называемое векторное пространство, используемое в современной математике, в физике, математической экономике и т.д.