Энтропия
Возможность предсказания направления процессов составляет основное содержание второго закона термодинамики. Немецкий физик Р. Клаузиус проанализировал ограничения, приводящие к односторонности процессов, и ввел функцию S, которую он назвал энтропией. В формулировке Клаузиуса (1865) второй закон термодинамики звучит так: «При самопроизвольных процессах в системах, имеющих постоянную энергию, энтропия всегда возрастает». Таким образом, система самопроизвольно переходит от условий A к условиям B, если SB > SA. В противном случае: — самопроизвольно происходит обратный процесс.
Существуют общие приемы расчета изменений энтропии при различных процессах, связанных с нагревом, охлаждением, плавлением, испарением, химическими реакциями и т. д. Эти приемы, рецепты расчетов составляют неотъемлемую часть термодинамики, и все они основаны на использовании тех или иных опытных данных. Например, чтобы рассчитать изменение энтропии при плавлении ∆Sпл, надо теплоту плавления λ разделить на температуру плавления Tпл. Для плавления 1 моля (18 г) льда λ = 6,02 кДж/моль, а Tпл = 273 К; соответственно ∆Sпл = 22 Дж/моль•град. Энтропия воды больше энтропии льда.
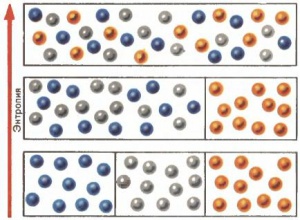
Австрийский физик Л. Больцман ответил на вопрос о физическом смысле энтропии и причинах её роста в изолированных системах (так называют системы, имеющие постоянную энергию). Согласно Больцману, энтропия — мера беспорядка в системе. Полный порядок соответствует минимуму энтропии; любой беспорядок увеличивает её. Таким образом, физический смысл возрастания энтропии следующий: будучи предоставленным самому себе, не испытывая внешних воздействий (изолированная система), коллектив частиц стремится перейти в состояние, в котором при данных условиях возможен больший беспорядок. Максимальная энтропия соответствует полному хаосу.
<addc>l</addc>
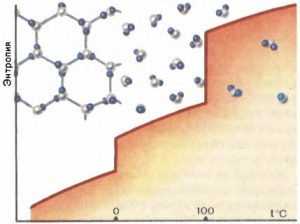
Спросим себя: где больше порядка в расположении атомов — в кристаллическом твердом теле, где атомы занимают определенные положения (узлы) в кристаллической решетке, или в жидкости, где определенных, закрепленных за ним положений у атома нет? Ответ ясен: в твердом теле. Поскольку энтропия — мера беспорядка, то в жидкости она больше, чем в кристалле; как уже говорилось, энтропия воды больше энтропии льда. Сравним теперь состояние частиц в водяном паре и в воде. Положения молекул не фиксированы и там, и там. Но при комнатной температуре и атмосферном давлении 1 моль воды (18 г) занимает объем 18 см3 (плотность воды составляет 1 г/см3), а 1 моль водяного пара — 22,4 л, т. е. в 1000 раз больше. Где возможен больший беспорядок? Конечно, в паре. И действительно, энтропия пара больше, чем энтропия воды, причем её изменение при испарении больше, чем при плавлении почти в 5 раз: A∆Sпл = 108 Дж/моль•град. Критерий максимума энтропии справедлив только для изолированных тел. Иначе все тела должны были быть газами. Если тело обменивается теплом с окружающей средой, то, согласно Гиббсу, устойчивому состоянию соответствуют наименьшие значения других термодинамических функций (см. Тепловое равновесие). Именно поэтому ниже температуры плавления устойчиво твердое состояние, между температурами плавления и кипения — жидкое и т. д.
Больцман впервые ввел понятие термодинамической «вероятности состояния системы», или числа способов, с помощью которых можно осуществить данное состояние. Согласно Больцману, различные комбинации скоростей и координат молекул, которые могут возникать в системе в результате столкновений между молекулами, не изменяют состояния системы в механическом смысле (энергия системы остается постоянной), но в термодинамическом смысле состояние системы будет изменяться. Всякая система, состоящая из очень большого числа частиц, будет переходить от состояний менее вероятных к состояниям более вероятным, осуществляющимся большим числом способов.
Связь между энтропией S и числом способов реализации данного состояния (термодинамической вероятностью) P дает известная формула Больцмана:
S = klnP + const,
где k = 1,38•10−23 Дж/град — постоянная Больцмана.