Тетраэдр
Тетраэдр, или треугольная пирамида, — простейший из многогранников, подобно тому как треугольник — простейший из многоугольников на плоскости. Слово «тетраэдр» образовано из двух греческих слов: tetra — «четыре» и hedra — «основание», «грань». Тетраэдр ABCD задается четырьмя своими вершинами — точками A, B, C, D, не лежащими в одной плоскости; грани тетраэдра — четыре треугольника; ребер у тетраэдра шесть. В отличие от произвольной n‑угольной пирамиды (при n ≥ 4) в качестве основания тетраэдра может быть выбрана любая его грань.
- Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения
Тетраэдр. Рис. 2.
- Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения
Тетраэдр. Рис. 6.
Многие свойства тетраэдров сходны с соответствующими свойствами треугольников. В частности, 6 плоскостей, проведенных через середины ребер тетраэдра перпендикулярно к ним, пересекаются в одной точке. В этой же точке O пересекаются и 4 прямые, проведенные через центры описанных около граней окружностей перпендикулярно к плоскостям граней, и O является центром описанной около тетраэдра сферы (рис. 1). Аналогично 6 биссекторных полуплоскостей тетраэдра, т. е. полуплоскостей, делящих двугранные углы при ребрах тетраэдра пополам, тоже пересекаются в одной точке — в центре вписанной в тетраэдр сферы — сферы, касающейся всех четырех граней тетраэдра. Любой треугольник имеет, вдобавок к вписанной, еще 3 вневписанные окружности (см. Треугольник), а вот тетраэдр может иметь любое число — от 4 до 7 вневписанных сфер, т. е. сфер, касающихся плоскостей всех четырех граней тетраэдра. Всегда существуют 4 сферы, вписанные в усеченные трехгранные углы, один из которых показан на рис. 2, справа. Ещё 3 сферы могут быть вписаны (не всегда!) в усеченные двугранные углы при ребрах тетраэдра — один из них показан на рис. 2, слева.
Для тетраэдра существует еще одна возможность его взаимного расположения со сферой — касание с некоторой сферой всеми своими ребрами (рис. 3). Такая сфера — иногда её называют «полувписанной» — существует лишь в том случае, когда суммы длин противоположных ребер тетраэдра равны: AB + CD = AC + BD = AD + BC (рис. 3).
Для любого тетраэдра справедлив аналог теоремы о пересечении медиан треугольника в одной точке. Именно, 6 плоскостей, проведенных через ребра тетраэдра и середины противолежащих ребер, пересекаются в одной точке — в центроиде тетраэдра (рис. 4). Через центроид M проходят также 3 «средние линии» — отрезки, соединяющие середины трех пар противоположных ребер, причем они делятся точкой M пополам. Наконец, через M проходят и 4 «медианы» тетраэдра — отрезки, соединяющие вершины с центроидами противолежащих граней, причем они делятся в точке M в отношении 3:1, считая от вершин.
Важнейшее свойство треугольника — равенство ∠A + ∠B + ∠C = 180° (или π) — разумного «тетраэдрического» аналога не имеет: сумма всех 6 двугранных углов тетраэдра может принимать любое значение между 2π и 3π. (Конечно, сумма всех 12 плоских углов тетраэдра — по 3 при каждой вершине — не зависит от тетраэдра и равна 4π.)
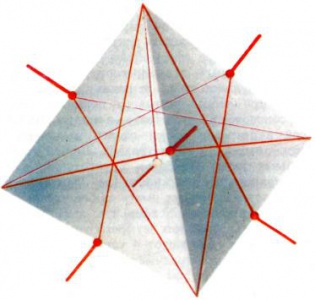
Треугольники принято классифицировать по степени их симметричности: правильные или равносторонние треугольники имеют три оси симметрии, равнобедренные — одну. Классификация тетраэдров по степени симметричности богаче. Самый симметричный тетраэдр — правильный, ограниченный четырьмя правильными треугольниками. Он имеет 6 плоскостей симметрии — они проходят через каждое ребро перпендикулярно противолежащему ребру — и 3 оси симметрии, проходящие через середины противолежащих ребер (рис. 5). Менее симметричны правильные треугольные пирамиды (3 плоскости симметрии, рис. 6) и равногранные тетраэдры (т. е. тетраэдры с равными гранями — 3 оси симметрии, рис. 7).
В заключение приведем две формулы для вычисления объема тетраэдра. Они не очень похожи на известные формулы для площади треугольника, но некоторую аналогию можно все-таки проследить.
где высота hD в данном случае есть расстояние от вершины D до плоскости грани ABC.
где (∠AB) — двугранный угол при ребре AB. Есть и другие формулы для вычисления объема тетраэдра.