Софизмы
Софизм — доказательство ложного утверждения, причем ошибка в доказательстве искусно замаскирована. Софистами называли группу древнегреческих философов IV-V вв. до н. э., достигших большого искусства в логике.
<addc>r</addc>
Приведем пример софизма. Если равны половины, то равны и целые. Полуполное есть то же, что и полупустое, значит, полное — то же самое, что пустое. К софизмам можно отнести доказательство того, что Ахиллес, бегущий в 10 раз быстрее черепахи, не сможет её догнать. Пусть черепаха на 100 м впереди Ахиллеса. Когда Ахиллес пробежит эти 100 м, черепаха будет впереди него на 10 м. Пробежит Ахиллес эти 10 м, а черепаха окажется впереди на 1 м и т. д. Расстояние между ними все время сокращается, но никогда не обращается в нуль. Значит, Ахиллес никогда не догонит черепаху.
А вот два математических софизма. «Докажем», что все числа равны между собой.
Пусть [math]a[/math] и [math]b[/math] — произвольные числа и пусть [math]a\gt b,[/math] тогда существует такое положительное число [math]c,[/math] что [math]a=b+c.[/math] Умножим это равенство на [math]a−b[/math] и преобразуем полученное равенство:
[math]a^2−ab=ab+ac−b^2−bc,[/math]
[math]a^2−ab−ac=ab−b^2−bc,[/math]
[math]a(a−b−c)=b(a−b−c).[/math]
Разделив обе части полученного равенства на [math](a−b−c),[/math] получим, что [math]a=b.[/math] Ошибка здесь находится в самом конце, когда мы делили на число [math](a−b−c),[/math] которое равно нулю.
А вот «доказательство» того, что все треугольники — равнобедренные.
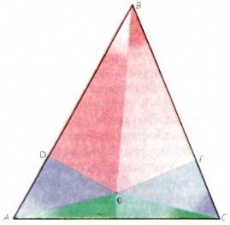
Рассмотрим произвольный треугольник [math]ABC[/math] (рис. 1). Проведем в нем биссектрису угла [math]B[/math] и серединный перпендикуляр к стороне [math]AC.[/math] Точку их пересечения обозначим через [math]O.[/math] Из точки [math]O[/math] опустим перпендикуляр [math]OD[/math] на сторону [math]AB[/math] и перпендикуляр [math]OE[/math] на сторону [math]BC.[/math] Очевидно, что [math]OA=OC[/math] и [math]OD=OE.[/math] Но тогда прямоугольные треугольники [math]AOD[/math] и [math]COE[/math] равны по катету и гипотенузе. Поэтому [math]∠DAO=∠ECO.[/math] В то же время [math]∠OAC=∠OCA,[/math] так как треугольник [math]AOC[/math] — равнобедренный. Получаем: [math]∠BAC=∠DAO+∠OAC= [/math][math]∠ECO+∠OCA=∠BCA.[/math]
Итак, угол [math]BAC[/math] равен углу [math]BCA,[/math] поэтому треугольник [math]ABC[/math] — равнобедренный: [math]AB=BC.[/math]
Здесь ошибка в чертеже. Серединный перпендикуляр к стороне и биссектриса противоположного ей угла для неравнобедренного треугольника пересекаются вне этого треугольника.
И еще один пример софизма. Посмотрим на рис. 2. Прямоугольники явно равносоставлены, но площадь одного равна 64 клеткам, а площадь другого — 65. И здесь ошибка в чертеже! Точки B, F и D не лежат на одной прямой, а являются вершинами очень узкого параллелограмма, площадь которого равна площади одной клетки — той самой лишней клетки.