Соотношение неопределенностей

В 1927 г. В. Гейзенберг, анализируя возможность измерения координаты и импульса электрона, пришел к заключению, что условия, благоприятные для измерения положения, затрудняют нахождение импульса, и наоборот — эти два понятия дополнительны друг другу. Для доказательства он ставил мысленные эксперименты: чтобы определить координату электрона, нужно осветить его и посмотреть в «микроскоп». Такой способ дает неопределенность координаты [math]Δq[/math] порядка длины волны [math]λ[/math] использованного света [math]Δq\simλ.[/math]

Схема перехода атома с энергией Е₂ в состояние с энергией Е₁ со средним временем жизни уровня 2, равным τ₂.

Для уточнения положения электрона надо брать возможно меньшую длину волны света. Но при взаимодействии с электроном свет передает ему импульс, который растет при уменьшении длины волны. Минимальный передаваемый электрону импульс будет порядка импульса одного фотона, а импульс фотона [math]{p}_{γ}[/math] связан с его длиной волны соотношением: [math]{p}_{γ}=2πħ/λ[/math] (здесь [math]ħ[/math] — постоянная Планка), поэтому неопределенность импульса электрона: [math]Δp\gt 2πħ/λ.[/math] Умножая на [math]λ[/math] и вместо [math]λ[/math] подставляя [math]Δq,[/math] получаем:

[math]ΔqΔp\gt 2πħ.[/math]

Это и есть соотношение неопределенностей Гейзенберга.

Проделав множество подобных мысленных экспериментов с тем же результатом, нельзя не прийти к заключению, что здесь речь идет о принципиальном ограничении, которое природа накладывает на понятия координаты и импульса частицы. Этого ограничения не знала классическая физика, оно не вносит изменения в описание макрообъектов из‑за очень малой величины постоянной Планка [math](ħ=1,05⋅{10}^{−34}[/math] Дж•с).

Помимо координаты и импульса существуют и другие величины, дополнительные друг другу. Угловое положение [math]φ[/math] вращающегося тела и его момент количества движения [math]М[/math] дополнительны. Их неопределенности связаны соотношением: [math]ΔφΔM\gt ħ.[/math]

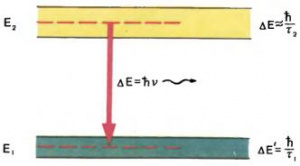
Как показал Н. Бор, аналогичное соотношение существует для произведения неопределенности энергии [math]ΔE[/math] и неопределенности момента взаимодействия [math]Δt[/math] объекта с измерительным прибором: [math]ΔEΔt_{\sim }^{\gt }ħ.[/math] Для пояснения этого соотношения сделаем еще один мысленный эксперимент.

Допустим, в экране, на который падает частица, имеется отверстие, достаточно широкое, чтобы пренебречь неопределенностью поперечного импульса, возникающего при прохождении частицы через экран. Пусть отверстие закрывается заслонкой на определенное время [math]Δt.[/math] Поскольку момент взаимодействия частицы с краями отверстия имеет неопределенность [math]Δt,[/math] то неопределенность координаты частицы в продольном направлении есть [math]Δq=vΔt,[/math] где [math]v[/math] — скорость частицы. Предполагается, что при прохождении отверстия скорость мало изменилась. Согласно соотношению неопределенностей Гейзенберга, неопределенность импульса частицы [math]Δp_{\sim }^{\gt }ħ/Δq=ħ/vΔt.[/math] Но неопределенность импульса создает неопределенность энергии [math]ΔE=vΔp=ħ/Δt,[/math] а это и есть соотношение неопределенностей Бора.

До сих пор говорилось о неопределенностях, которые возникают в акте измерения. В этих случаях уравнение Шрёдингера неприменимо для описания частицы хотя бы потому, что она не изолирована, а взаимодействует с другой системой, играющей роль измерительного прибора.

Есть соотношение неопределенностей, имеющее другой физический смысл. Пусть частица находится в определенном состоянии, описываемом волновой функцией, которая удовлетворяет уравнению Шрёдингера. В этом состоянии интервалы возможных значений дополнительных величин (например, средние квадратичные отклонения импульса и координаты частицы от их средних значений) будут удовлетворять соотношению неопределенностей.

Так, в основном состоянии атома водорода волновая функция дает интервал возможных значений координаты электрона, который связан с интервалом возможных значений импульса соотношением: [math]ΔpΔq_{\sim }^{\gt }ħ.[/math] Отсюда можно оценить радиус атома [math]a,[/math] характеризующий интервал возможных значений координаты. В основном состоянии потенциальная энергия электрона [math]e^2/a[/math] должна быть примерно равна кинетической энергии [math]p^2/2m[/math] (где [math]p[/math] по порядку величины равно возможному значению импульса [math]p∼ħ/a[/math]). Приравнивая эти две энергии, получаем оценку для радиуса атома [math]a=ħ^2me^2[/math] и для энергии ионизации [math]I=me^4/ħ^2.[/math]

Атом в возбужденном состоянии имеет неопределенную энергию. Эта неопределенность объясняется переходом на нижние уровни, сопровождающимся испусканием кванта. Неопределенность энергии связана соотношением Бора со временем жизни атома [math]τ[/math] по отношению к испусканию света: [math]ΔEτ_{\sim }^{\gt }\lt /sub\gt ħ.[/math]

<addc>r</addc>

Соотношение неопределенностей — частный случай и конкретное выражение общего принципа дополнительности, сформулированного Н. Бором в 1927 г. Именно этот принцип позволяет примирить, казалось бы, непримиримое: ведь электрон проявляет себя в различных экспериментах то как частица, то как волна. Квантовая механика осуществляет синтез этих понятий и дает возможность предсказать исход любого опыта, в котором проявляются как корпускулярные, так и волновые свойства частиц.

Принцип дополнительности Бор применял во многих областях. Так, например, физическая картина явления и его математическое описание дополнительны. Создание физической картины требует пренебрежения деталями и уводит от математической точности, а попытка точного математического описания явления затрудняет его ясное понимание.

Квантовая механика не дает однозначного ответа на некоторые вопросы, а лишь предсказывает вероятность того или иного результата. Классическая физика не знала неопределенности. Если задать координаты и. скорости механической системы, то можно однозначно предсказать все её поведение. В то же время, как следует из соотношения неопределенностей, задать координаты и скорости всех частиц невозможно, есть возможность лишь задать в начальный момент волновую функцию системы. Квантовая механика позволяет найти её в любой следующий момент.

Невозможность однозначно предсказать исход опыта была настолько непривычной, что вызвала множество возражений. Достаточно ли полно квантовомеханическое описание, или нужно создать более точную теорию? Многолетний спор Бора с Эйнштейном по этому поводу привел к углублению и уточнению понятий квантовой физики.

Особенность квантовой механики состоит в том, что свойства микроскопических объектов нельзя изучать, отвлекаясь от способа наблюдения. В зависимости от него электрон проявляет себя либо как волна, либо как частица, либо как нечто промежуточное. Конечно, существуют свойства, не зависящие от способа наблюдения: масса, заряд, спин частицы… Но всякий раз, когда мы хотим одновременно измерить дополнительные друг другу величины — такие, как координата и скорость, результат будет зависеть от способа наблюдения.

Принципиальная неопределенность некоторых величин есть следствие применения классических понятий к описанию неклассических объектов. Квантовая природа микрообъектов дополнительна их классическому описанию.