Равновеликие и равносоставленные фигуры
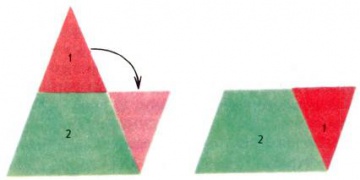
При вычислении площадей многоугольников используется простой прием, называемый методом разбиения. Рассмотрим многоугольники F и H, изображенные на рис. 1, где показано, как разбить эти многоугольники на одинаковое число соответственно равных частей (равные части отмечены одинаковыми цифрами). О многоугольниках F и H говорят, что они равносоставлены. Вообще, многоугольники A и B называются равносоставленными, если, определенным образом разрезав многоугольник A на конечное число частей, можно, располагая эти части иначе, составить из них многоугольник B. Легко видеть, что справедлива следующая теорема: равносоставленные многоугольники имеют одинаковую площадь, или, как говорят, равновелики. Например, параллелограмм равносоставлен с прямоугольником (рис. 2), и потому, зная формулу площади прямоугольника, находим, что площадь параллелограмма равна произведению длин его стороны и соответствующей высоты.
Равновеликие и равносоставленные фигуры. Рис. 1.
Равновеликие и равносоставленные фигуры. Рис. 2.
Равновеликие и равносоставленные фигуры. Рис. 3.
Равновеликие и равносоставленные фигуры. Рис. 4.
Равновеликие и равносоставленные фигуры. Рис. 5.
Этот пример иллюстрирует метод разбиения, состоящий в том, что для вычисления площади многоугольника пытаются разбить его на конечное число частей таким образом, чтобы из этих частей можно было составить более простой многоугольник, площадь которого нам уже известна. Например, треугольник равносоставлен с параллелограммом, имеющим то же основание и вдвое меньшую высоту (рис. 3); из этого легко выводится формула площади треугольника. Этот способ вычисления площадей многоугольников был известен еще Евклиду, который жил более 2000 лет назад.
Замечательно, что для приведенной выше теоремы справедлива и обратная теорема: если два многоугольника равновелики, то они равносоставлены. Эту теорему, доказанную в первой половине XIX в. венгерским математиком Ф. Бойяи и немецким офицером и любителем математики П. Гервином, можно пояснить так: если имеется пряник в форме многоугольника и многоугольная коробка совершенно другой формы, но той же площади, то можно так разрезать пряник на конечное число кусков, что их удастся вложить в эту коробку.
В связи с теоремой Бойяи‑Гервина возникает вопрос о наложении дополнительных ограничений на число или расположение частей, из которых составляются равновеликие многоугольники. Например, представим себе плоскость в виде листа цветной бумаги, у которого одна сторона красная, а другая — белая. Если из такой бумаги вырезаны два равновеликих красных многоугольника, то возникает вопрос, можно ли один из них разрезать на части, из которых удастся сложить красный многоугольник, равный второму. Части разрешается перекладывать, не переворачивая их на белую, изнаночную сторону. Ответ на этот вопрос также утвердителен.
Вариант этой задачи был предложен на одной из московских математических олимпиад в следующей шуточной форме. Чудак — кондитер испек торт (а у торта, в отличие от пряника, верхняя сторона покрыта кремом) в форме разностороннего треугольника. Сделали и коробку к торту, но по недосмотру склеили её неверно, так что торт и коробка оказались симметричными друг другу (рис. 4). Нужно (по возможности экономно) разрезать торт на части, которые удалось бы уложить в эту коробку. Разумеется, части торта нельзя укладывать кремом вниз.
<addc>G</addc>
Интересный результат, связанный с наложением дополнительных требований на расположение частей, был получен в 1952 г. швейцарскими математиками Г. Хадвигером и П. Глюром: равносоставленность двух равновеликих многоугольников может быть установлена при помощи таких разбиений, в которых соответствующие части имеют параллельные стороны. На первый взгляд это кажется даже неправдоподобным: трудно поверить, что два равных треугольника, повернутые друг относительно друга на произвольный угол (рис. 5), всегда можно разбить на равные части с соответственно параллельными сторонами. Тем не менее существует такое разбиение этих треугольников, что части, на которые разбит один треугольник, получаются из соответствующих частей второго треугольника параллельными переносами или центральными симметриями. То же справедливо для любых двух равновеликих многоугольников. Однако одними только параллельными переносами частей обойтись не удается. Например, как бы мы ни разрезали параллелограмм на части, невозможно параллельными переносами составить из этих частей треугольник.
Интерес к этим вопросам был пробужден знаменитым докладом «Математические проблемы», который был прочитан выдающимся математиком Д. Гильбертом на Втором Международном конгрессе математиков, состоявшемся на рубеже XIX и XX вв. Из двадцати трех поставленных Гильбертом проблем большинство относится к новым, быстро развивающимся разделам математики. И лишь одна проблема — третья — связана с вопросами школьной геометрии. Гильберт обращает внимание на то, что при вычислении объема треугольной пирамиды еще со времен Евклида используется довольно сложный предельный переход (см. Предел) (а в настоящее время — интегрирование), тогда как при вычислении площади треугольника мы обходимся без аналогичного предельного перехода. Существо проблемы Гильберта состоит в том, чтобы обосновать использование этого «лишнего» (по сравнению с планиметрией) предельного перехода, т. е. доказать, что без него теория объемов многогранников не может быть построена. В 1900 г. М. Ден решил третью проблему Гильберта, доказав, что правильный тетраэдр и равновеликий ему куб не равносоставлены. Гильберт предвидел, что этот вопрос может привести к созданию математически интересной и богатой результатами теории равносоставленности многоугольников и многогранников. Предвидение Гильберта блестяще оправдалось; красивое здание современной теории равносоставленности является достойным памятником ученому.
