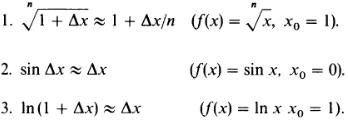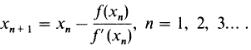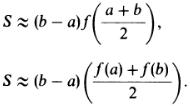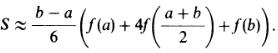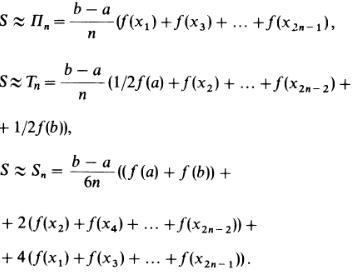Приближенные вычисления

В практической деятельности мы постоянно имеем дело с приближенными величинами, равенствами, формулами: строим по точкам графики, извлекаем корни из чисел, решаем уравнения и т. д. В теории приближенных вычислений, которая в наши дни быстро развивается, особое значение имеют методы, пригодные для решения широкого класса математических задач. Расскажем о некоторых таких методах.

Вычисление длины окружности при помощи формул удвоения — конкретный пример алгоритма для получения приближенных значений числа π. Этот метод интересен и с исторической точки зрения, так как, возможно, это один из самых старых приемов приближенных вычислений. Формула удвоения связывает длины сторон a_n и a_2n правильных n- и 2n-угольников, вписанных в окружность (диаметр равен 1):

и позволяет, начав с правильного шестиугольника, длина стороны которого равна 1/2, вычислять последовательно a₁₂, a₂₄, a₄₈, …, пока не придем к значению периметра, отвечающему заданной точности вычислений. При этом можно доказать, что

π − na_n < 6/n², n ≥ 3.

Это неравенство позволяет не только установить тот факт, что процесс сходится (т. е. π − na_n → 0 при n → ∞), но и спланировать вычисления заранее. Так, если нам нужно обеспечить точность вычислений, равную 10⁻³, то достаточно взять n таким, чтобы выполнялось неравенство 6/n² < 10⁻³, т. е. n > √6000, или n ≥ 78 > √6000.

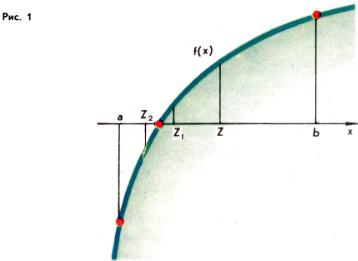
Метод вилки, применяемый при нахождении корней уравнения f(x) = 0 для непрерывных функций f, носит довольно общий характер. Пусть f определена и непрерывна на отрезке [a, b], имеет там единственный корень и f(a) < 0, f(b) > 0. Рассмотрим значение f(z), где z = (a + b)/2 — середина отрезка [a, b]. Если f(z) = 0, то z — искомый корень. Если же f(z) ≠ 0, то из двух отрезков [a, z] и [z, b] выберем тот, для которого значения функции f на его концах имеют разные знаки (на рис. 1 это отрезок [a, z]), и обозначим его через [a₁, b₁] тем самым f(a₁) < 0 и f(b₁) > 0. Если теперь взять точку z₁ = (a₁ + b₁)/2, то снова или f(z₁) = 0, или f(z₁) ≠ 0. Во втором случае из двух отрезков [a₁, z₁] и [z₁, b₁] выбираем тот, на концах которого функция f принимает значения разных знаков (на рис. 1, [a₂, b₂] = [a, z₁]). Если мы будем продолжать этот процесс, то он или оборвется на некотором шаге, или мы получим последовательность вложенных отрезков [a, b], [a₁, b₁] [a₂, b₂], …, для которых a_n ≤ a_n+1 < b_n+1 ≤ b_n, причем всегда f(a_n) < 0 и f(b_n) > 0. Из геометрических соображений ясно, что

Кроме того, имеем неравенства:

которые позволяют планировать расчеты с заданной точностью.

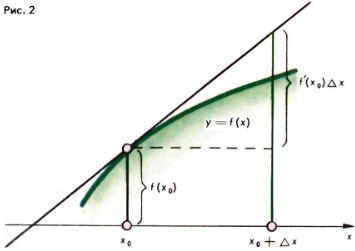
Применение производной при изучении поведения функции позволяет получить много полезных формул для приближенного вычисления значений функций. Из определения производной следует, что при малых приращениях ∆x аргумента x₀ для функции f можно написать приближенное равенство

f(x₀ + ∆x) ≈ f(x₀) + f ′(x₀)∆x.

Геометрически это означает, что вблизи точки x = x₀ мы график функции y = f(x) заменили графиком касательной к графику y = f(x) в точке с абсциссой x = x₀ (рис. 2).

Так, например, получаются приближенные формулы (эффективные для малых ∆х):

Метод касательных Ньютона для приближенного решения уравнений f(x) = 0 состоит в следующем. Предположим, что функция f имеет единственный корень c в интервале ]a, b[ и дифференцируема в каждой точке интервала ]a, b[ и f ′ ≠ 0 в этом интервале. Возьмем произвольную точку x₀ ∈ ]a, b[ и напишем уравнение касательной к графику функции f в точке с абсциссой x = x₀:

y = f ′(x₀)(x − x₀) + f(x₀).

Графики f(x) и её касательной близки между собой при малых x − x₀, и поэтому естественно ожидать, что точка x₁ пересечения графика касательной с осью абсцисс будет расположена недалеко от корня c (рис. 2). Имеем:

Продолжая этот процесс, мы получим последовательность (x_n) точек, определенных при помощи формулы

Известно, что имеет место также неравенство

|x_n+1 − c| ≤ A•|x_n − c|²,

где A > 0 — некоторая постоянная, не зависящая от n. Это неравенство показывает, что уже при достаточно малых n получается достаточно высокая точность приближений.

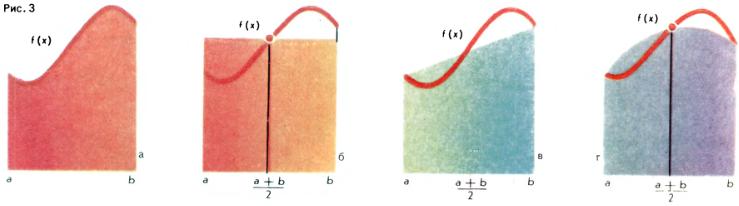
Приближенное вычисление площадей (интегралов) криволинейных трапеций (рис. 3, а) основано на простых геометрических рассмотрениях. Если отрезок [a, b], a < b, достаточно мал, то для вычисления площади S криволинейной трапеции для заданной непрерывной функции f на этом отрезке можно, заменив криволинейную трапецию прямоугольником (рис. 3, б) или прямолинейной трапецией (рис. 3, в), написать следующие приближенные равенства:

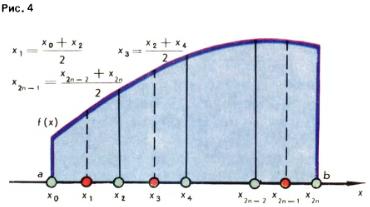
Если заменить график функции на отрезке [a, b] не прямолинейным отрезком, а графиком параболы (рис. 3, г) и в качестве приближения для S взять площадь криволинейной трапеции, ограниченной дугой этой параболы, то получим формулу

Интегральное исчисление дает возможность более точно вычислить площадь криволинейной трапеции.

Чтобы добиться возможно меньшей ошибки при приближенных вычислениях S, промежуток от a до b разбивают предварительно на 2n равных частей. Тогда дуга графика y = f(x) разбивается на n частей (рис. 4). Если теперь для каждой из этих маленьких дуг использовать предыдущие способы приближения, то для площади S получатся приближенные значения в виде сумм площадей n криволинейных трапеций; имеем:

Первые две формулы носят названия формулы прямоугольников и формулы трапеций, а последняя — формулы Симпсона, по имени английского математика Т. Симпсона (1710–1761).

Оценки погрешности в этих приближенных формулах на практике подсчитываются следующим образом. Выбирают число n, кратное 4, и находят значение S по формуле Симпсона (более точной из этих трех) с числом точек n и n/2 (S_n и S_n/2) и приближенно определяют ошибку вычислений при помощи соотношения

S − S_n ≈ 1/15(S_n − S_n/2).