Потенциальная энергия
Еще в древности было открыто золотое правило механики: выигрывая в силе, проигрываешь в расстоянии. Действительно, если, например, поднимать груз по наклонной плоскости, то приходится совершать работу против сил тяжести (будем считать, что работой против сил трения можно пренебречь). Если наклонная плоскость пологая, то путь длинный, но к грузу можно прикладывать меньшую силу. По крутой плоскости поднимать груз тяжелее, но зато путь короче. Работа, которую надо совершить для того, чтобы поднять груз массы [math]m[/math] на высоту [math]h,[/math] всегда одинакова и равна [math]mgh.[/math]
Рис. 1. Работа по_перемещению тела в_поле тяжести не_зависит от_формы пути.
Рис. 2. На_больших расстояниях атомы притягиваются друг к_другу.
Рис. 3. График потенциальной энергии взаимодействия двух атомов.
Рис. 4. Положение равновесия шарика на_кривой поверхности.
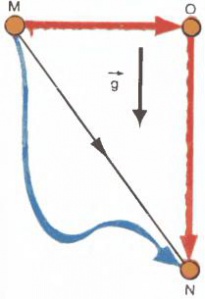
Это важнейшее свойство сил тяжести: работа не зависит от формы пути, а определяется только начальным и конечным положениями тела. На рис. [math]1[/math] показаны три возможных перемещения тела из точки [math]M[/math] в точку [math]N.[/math] Ускорение поля тяжести [math]\overrightarrow{g}[/math] обозначено стрелкой. Легко доказать, что, перемещая тела по отрезку [math]MN[/math] и по ломаной [math]MON,[/math] придется совершить одинаковую работу, так как на участке [math]MO[/math] работа равна нулю. Разбив кривой путь на множество прямых отрезков, можно убедиться, что в этом случае работа одинаковая.
Силы, обладающие таким свойством, называют потенциальными или консервативными. Для них можно определить потенциальную энергию. Достаточно выбрать начало отсчета — считать, что в каком‑то положении (например, на поверхности Земли) потенциальная энергия равна нулю, и тогда в любой другой точке она будет равна работе по перемещению тела из начального положения в эту точку.
Потенциальная энергия вместе с кинетической энергией составляет полную механическую энергию тела. Если тело находится только в поле потенциальных сил, то полная энергия сохраняется (закон сохранения механической энергии). Чтобы запустить ракету, способную покинуть пределы Солнечной системы, необходимо сообщить ей огромную скорость (около [math]11[/math] км/с). Запас кинетической энергии компенсирует увеличение потенциальной энергии при удалении ракеты от Земли.
<addc>l</addc>
Потенциальны не только силы тяжести, но и силы электростатического взаимодействия. Ведь закон Кулона очень похож на закон всемирного тяготения Ньютона. Даже формулы для потенциальной энергии почти одинаковые: в обоих случаях энергия обратно пропорциональна расстоянию между взаимодействующими телами.
В то же время работа сил трения зависит от формы пути (например, при сухом трении короткий путь самый лучший), и такие силы не являются потенциальными.
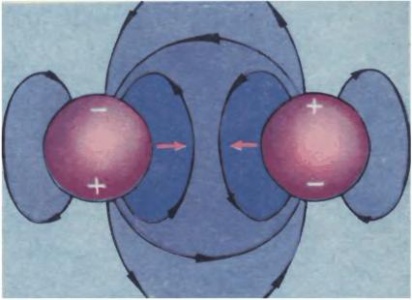
С помощью потенциальной энергии удобно описывать взаимодействие частиц в микромире, например двух атомов. На больших расстояниях между атомами действуют силы притяжения. Хотя каждый атом нейтральный, под воздействием электрического поля другого атома он превращается в маленький диполь, и эти диполи притягиваются друг к другу (рис. [math]2[/math]). Поэтому при сближении атомов их надо удерживать и совершать отрицательную работу против этих сил. На малых расстояниях между атомами, напротив, действуют силы отталкивания, обусловленные в основном кулоновским взаимодействием сближающихся ядер. В этом случае для сближения атомов надо совершать положительную работу.
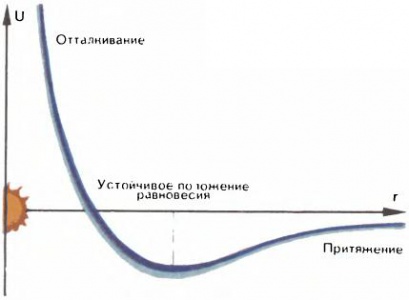
График потенциальной энергии атомов в зависимости от расстояния между ними показан на рис. [math]3[/math]. Потенциальная энергия имеет минимум, и это положение атомов соответствует устойчивому образованию — молекуле. В таком случае говорят, что атомы находятся в потенциальной яме.
Точно так же в кристалле атомы располагаются в пространстве таким образом, чтобы он обладал минимальной потенциальной энергией. В результате образуется периодическая структура — кристаллическая решетка (см. Кристаллофизика).
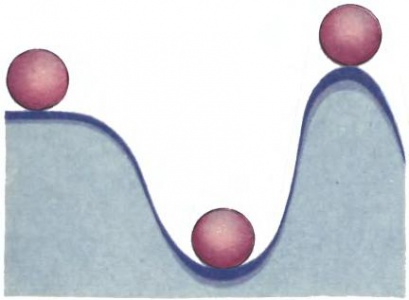
Устойчивому положению системы всегда соответствует минимум потенциальной энергии. На рис. [math]4[/math] показан рельеф поверхности, на которой находится шарик. Имеется три положения равновесия, но только одно, соответствующее минимуму потенциальной энергии, — устойчивое (в данном случае шарик буквально в яме).
Интересно, что если между частицами действуют только силы электростатического взаимодействия (система неподвижных зарядов), то они вообще не могут находиться в состоянии устойчивого равновесия. Потенциальная энергия не имеет минимума, и система обязательно развалится (заряды разлетятся). Эта теорема Ирншоу послужила важнейшим доказательством несостоятельности статической модели атома.
