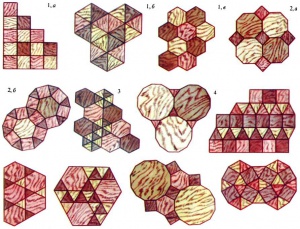
Паркеты из правильных многоугольников
Самый простой, но и самый скучный паркет получается, если плоскость разбить на равные квадраты так, как показано на рис. 1,а. Здесь два квадрата имеют либо общую сторону, либо общую вершину или совсем не имеют общих точек. Столь же просты паркеты из правильных треугольников и шестиугольников (рис. 1,б и 1,в).
Паркетом будем называть такое покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину или совсем не имеют общих точек.
<addc>l</addc>
Вероятно, вам случалось видеть паркет, составленный из правильных восьмиугольников и квадратов (рис. 2,а). Красивый паркет можно составить из правильных шестиугольников, квадратов и равносторонних треугольников (рис. 2,б).
Паркет производит приятное впечатление, если он достаточно симметричен. Фигура называется симметричной, если её можно наложить на саму себя не «тривиальным» способом (т.е. не таким, когда все точки останутся на своем месте).
Например, на рис. 2,б, повернув всю сетку вершин и сторон, образующих паркет из шестиугольников, квадратов и треугольников, на 60° вокруг центра одного из шестиугольников, мы получим ту же самую сетку вершин и сторон.
С точки зрения симметрии наше определение паркета не слишком удачно. Оно допускает паркеты, не обладающие никакой симметрией. Взяв обычный паркет из шестиугольников (рис. 1,в), можно «испортить» его, подразделив некоторые из шестиугольников на шесть треугольников. Легко понять, что получится вновь паркет в смысле нашего определения. Но можно доказать (попробуйте), что, подразделив, например, три шестиугольника, как показано на рис. 3, и оставив все остальные неподразделенными, мы получим паркет, совсем лишенный симметрии. Чтобы устранить некрасивые, недостаточно симметричные паркеты, мы введем такое определение: паркет называется правильным, если его можно наложить на самого себя так, что любая заданная его вершина наложится на любую другую заданную его вершину. Оказывается, что все многообразие правильных паркетов можно описать. Если длина h стороны многоугольников паркета задана, то существует только 11 различных (не накладывающихся друг на друга) правильных паркетов. Все они изображены на рис. 1, 2, 4.