Окружность и круг
Формы круга, окружности мы встречаем повсюду: это и колесо машины, и линия горизонта, и диск Луны. Математики стали заниматься геометрической фигурой — кругом на плоскости — очень давно.
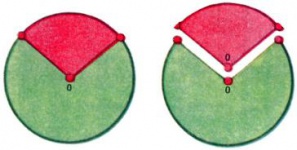
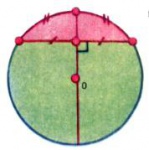
Кругом с центром [math]O[/math] и радиусом [math]R[/math] называется множество точек плоскости, удаленных от [math]O[/math] на расстояние, не большее [math]R.[/math] Круг ограничен окружностью, состоящей из точек, удаленных от центра [math]O[/math] в точности на расстояние [math]R.[/math] Отрезки, соединяющие центр с точками окружности, имеют длину [math]R[/math] и также называются радиусами (круга, окружности). Части круга, на которые он делится двумя радиусами, называются круговыми секторами (рис. 1). Хорда — отрезок, соединяющий две точки окружности, — делит круг на два сегмента, а окружность — на две дуги (рис. 2). Перпендикуляр, проведенный из центра к хорде, делит её и стягиваемые ею дуги пополам. Хорда тем длиннее, чем ближе она расположена к центру; самые длинные хорды — хорды, проходящие через центр, — называются диаметрами (круга, окружности).
Если прямая удалена от центра круга на расстояние [math]d,[/math] то при [math]d \gt R[/math] она не пересекается с кругом, при [math]d \lt R[/math] пересекается с кругом по хорде и называется секущей, при [math]d=R[/math] имеет с кругом и окружностью единственную общую точку и называется касательной. Касательная характеризуется тем, что она перпендикулярна радиусу, проведенному в точку касания. К кругу из точки, лежащей вне его, можно провести две касательные, причем их отрезки от данной точки до точек касания равны.
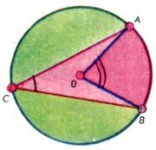
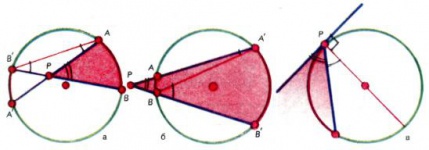
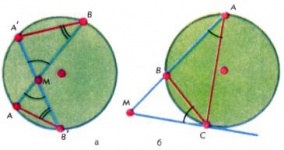
Дуги окружности, как и углы, можно измерять в градусах и его долях. За градус принимают [math]1/360[/math] часть всей окружности. Центральный угол [math]AOB[/math] (рис. 3) измеряется тем же числом градусов, что и дуга [math]AB,[/math] на которую он опирается; вписанный угол [math]ACB[/math] измеряется половиной дуги [math]AB.[/math] Если вершина [math]P[/math] угла [math]APB[/math] лежит внутри круга, то этот угол в градусной мере равен полусумме дуг [math]AB[/math] и [math]A′B′[/math] (рис. 4, а). Угол с вершиной [math]P[/math] вне круга (рис. 4, б), высекающий на окружности дуги [math]AB[/math] и [math]A′B′,[/math] измеряется полуразностью дуг [math]A′B′[/math] и [math]AB.[/math] Наконец, угол между касательной и хордой равен половине заключенной между ними дуги окружности (рис. 4, в).
Круг и окружность имеют бесконечное множество осей симметрии.
Из теорем об измерении углов и подобия треугольников следуют две теоремы о пропорциональных отрезках в круге. Теорема о хордах говорит, что если точка [math]М[/math] лежит внутри круга, то произведение длин отрезков [math]AM⋅BM[/math] проходящих через нее хорд постоянно. На рис. 5, а [math]AM⋅BM=A′M′⋅B′M.[/math] Теорема о секущей и касательной (имеются в виду длины отрезков - частей этих прямых) утверждает, что если точка [math]М[/math] лежит вне круга, то произведение секущей [math]МА[/math] на её внешнюю часть [math]MB[/math] тоже неизменно и равно квадрату касательной [math]MC[/math] (рис. 5, б).
<addc>l</addc>
Еще в древности пытались решить задачи, связанные с кругом, — измерить длину окружности или её дуги, площадь круга или сектора, сегмента. Первая из них имеет чисто «практическое» решение: можно уложить вдоль окружности нить, а потом развернуть её и приложить к линейке или же отметить на окружности точку и «прокатить» её вдоль линейки (можно, наоборот, «обкатить» линейкой окружность). Так или иначе измерения показывали, что отношение длины окружности [math]L[/math] к её диаметру [math]d=2R[/math] одно и то же для всех окружностей. Это отношение принято обозначать греческой буквой [math]π[/math] («пи» — начальная буква греческого слова perimetron, которое и означает «окружность»).
Однако древнегреческих математиков такой эмпирический, опытный подход к определению длины окружности не удовлетворял: окружность — это линия, т.е., по Евклиду, «длина без ширины», а таких нитей не бывает. Если же мы катим окружность по линейке, то возникает вопрос: почему при этом мы получим длину окружности, а не какую‑нибудь другую величину? К тому же такой подход не позволял определить площадь круга.
Выход был найден такой: если рассмотреть вписанные в круг [math]K[/math] правильные [math]n[/math]‑угольники [math]M_n,[/math] то при [math]n,[/math] стремящемся к бесконечности, [math]M_n[/math] в пределе стремятся к [math]K.[/math] Поэтому естественно ввести следующие, уже строгие, определения: длина окружности [math]L[/math] — это предел последовательности периметров [math]P_n[/math] правильных вписанных в окружность [math]n[/math]‑угольников, а площадь круга [math]S[/math] — предел последовательности [math]S_n[/math] их площадей. Такой подход принят и в современной математике, причем по отношению не только к окружности и кругу, но и к другим кривым или ограниченным криволинейными контурами областям: вместо правильных многоугольников рассматривают последовательности ломаных с вершинами на кривых или контурах областей, а предел берется при стремлении длины наибольшего звена ломаной к нулю.
Аналогичным образом определяется длина дуги окружности: дуга делится на n равных частей, точки деления соединяются ломаной и длина дуги [math]L[/math] полагается равной пределу периметров [math]l_n[/math] таких ломаных при [math]n,[/math] стремящемся к бесконечности. (Подобно древним грекам, мы не уточняем само понятие предела — оно относится уже не к геометрии и было вполне строго введено лишь в XIX в.)
Из самого определения числа π следует формула для длины окружности:
[math]L=πd=2πR.[/math]
Для длины дуги можно записать аналогичную формулу: поскольку для двух дуг [math]Γ[/math] и [math]Γ′[/math] с общим центральным углом из соображений подобия вытекает пропорция [math]l_n:l′_n=R:R′,[/math] а из нее — пропорция [math]l_n:R=l′_n:R′,[/math] после перехода к пределу мы получаем независимость (от радиуса дуги) отношения [math]l/R=l′/R′=α.[/math] Это отношение определяется только центральным углом [math]AOB[/math] и называется радианной мерой этого угла и всех отвечающих ему дуг с центром в [math]O.[/math] Тем самым получается формула для длины дуги:
[math]l=αR,[/math]
где [math]α[/math] — радианная мера дуги.
Записанные формулы для [math]L[/math] и [math]l[/math] — это всего лишь переписанные определения или обозначения, но с их помощью получаются уже далекие от просто обозначений формулы для площадей круга и сектора:
[math]S=πR^2,[/math] [math]S=\frac{1}{2}αR^2.[/math]
Для вывода первой формулы достаточно перейти к пределу в формуле для площади вписанного в круг правильного n‑угольника:
[math]S_n=\frac{1}{2}P_nh_n.[/math]
По определению левая часть стремится к площади круга [math]S,[/math] а правая — к числу
[math]\frac{1}{2}LR=\frac{1}{2}⋅2πR⋅R =πR^2[/math]
(апофема [math]h_n,[/math] конечно, стремится к [math]R[/math]). Совершенно аналогично выводится и формула для площади сектора [math]s[/math]:
[math]s=\lim S_n=\lim (\frac{1}{2}l_nh_n)=[/math] [math]\frac{1}{2}\lim l_n⋅\lim h_n=[/math] [math]\frac{1}{2}lR=[/math] [math]\frac{1}{2}αR^2[/math]
([math]\lim [/math]— читается «предел»). Тем самым решена и задача определения площади сегмента с хордой [math]AB,[/math] ибо она представляется как разность или сумма (рис. 1, 2) площадей соответствующих сектора и треугольника [math]AOB.[/math]