Обратные тригонометрические функции

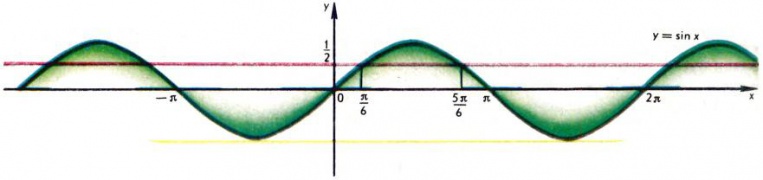
В ряде задач математики и её приложений требуется по известному значению тригонометрической функции найти соответствующее значение угла, выраженное в градусной или в радианной мере. Известно, что одному и тому же значению синуса соответствует бесконечное множество углов, например, если [math]\sin α=1/2,[/math] то угол [math]α[/math] может быть равен и [math]30°[/math] и [math]150°,[/math] или в радианной мере [math]π/6[/math] и [math]5π/6,[/math] и любому из углов, который получается из этих прибавлением слагаемого вида [math]360°⋅k,[/math] или соответственно [math]2πk,[/math] где [math]k[/math] — любое целое число. Это становится ясным и из рассмотрения графика функции [math]y=\sin x[/math] на всей числовой прямой (см. рис. [math]1[/math]): если на оси [math]Oy[/math] отложить отрезок длины [math]1/2[/math] и провести прямую, параллельную оси [math]Ox,[/math] то она пересечет синусоиду в бесконечном множестве точек. Чтобы избежать возможного разнообразия ответов, вводятся обратные тригонометрические функции, иначе называемые круговыми, или аркфункциями (от латинского слова arcus — «дуга»).

• 

  Рис. 1.

• 

  Рис. 2.

• 

  Рис. 3.

Основным четырем тригонометрическим функциям [math]\sin x,[/math] [math]\cos x,[/math] [math]\mathrm{tg}\,x[/math] и [math]\mathrm{ctg}\,x[/math] соответствуют четыре аркфункции [math]\arcsin x,[/math] [math]\arccos x,[/math] [math]\mathrm{arctg}\,x[/math] и [math]\mathrm{arcctg}\,x[/math] (читается: арксинус, арккосинус, арктангенс, арккотангенс). Рассмотрим функции \arcsin x и \mathrm{arctg}\,x, поскольку две другие выражаются через них по формулам:

[math]\arccos x = \frac{π}{2} − \arcsin x,[/math] [math]\mathrm{arcctg}\,x = \frac{π}{2} − \mathrm{arctg}\,x.[/math]

<addc>l</addc>

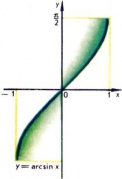
Равенство [math]y = \arcsin x[/math] по определению означает такой угол [math]y,[/math] выраженный в радианной мере и заключенный в пределах от [math]−\frac{π}{2}[/math] до [math]\frac{π}{2},[/math] синус которого равен [math]x,[/math] т. е. [math]\sin y = x.[/math] Функция [math]\arcsin x[/math] является функцией, обратной функции [math]\sin x,[/math] рассматриваемой на отрезке [math]\left[−\frac{π}{2},+\frac{π}{2}\right],[/math] где эта функция монотонно возрастает и принимает все значения от [math]−1[/math] до [math]+1.[/math] Очевидно, что аргумент [math]y[/math] функции [math]\arcsin x[/math] может принимать значения лишь из отрезка [math]\left[−1,+1\right].[/math] Итак, функция [math]y=\arcsin x[/math] определена на отрезке [math]\left[−1,+1\right],[/math] является монотонно возрастающей, и её значения заполняют отрезок [math]\left[−\frac{π}{2},+\frac{π}{2}\right].[/math] График функции показан на рис. [math]2.[/math]

При условии [math]−1 ≤ a ≤ 1[/math] все решения уравнения [math]\sin x = a[/math] представим в виде [math]x=(−1)^n \arcsin a + πn,[/math] [math]n=0,±1,± 2,… .[/math] Например, если

[math]\sin x = \frac{\sqrt{2}}{2}[/math] то [math]x = (−1)^n \frac{π}{4}+πn,[/math] [math]n = 0, ±1, ±2, … .[/math]

Соотношение [math]y=\mathrm{arcctg}\,x[/math] определено при всех значениях [math]x[/math] и по определению означает, что угол [math]y,[/math] выраженный в радианной мере, заключей в пределах

[math]−\frac{π}{2} \lt y \lt \frac{π}{2}[/math]

и тангенс этого угла равен x, т. е. [math]\mathrm{tg}\,y = x.[/math] Функция [math]\mathrm{arctg}\,x[/math] определена на всей числовой прямой, является функцией, обратной функции [math]\mathrm{tg}\,x[/math], которая рассматривается лишь на интервале

[math]−\frac{π}{2} \lt x \lt \frac{π}{2}.[/math]

Функция [math]у = \mathrm{arctg}\,x[/math] монотонно возрастающая, её график дан на рис. [math]3.[/math]

Все решения уравнения [math]\mathrm{tg}\,x = a[/math] могут быть записаны в виде [math]x=\mathrm{arctg}\,a+πn,[/math] [math]n=0,±1,±2,… .[/math]

Заметим, что обратные тригонометрические функции широко используются в математическом анализе. Например, одной из первых функций, для которых было получено представление бесконечным степенным рядом, была функция [math]\mathrm{arctg}\,x.[/math] Из этого ряда Г. Лейбниц при фиксированном значении аргумента [math]x=1[/math] получил знаменитое представление числа к бесконечным рядом

[math]π=4(1−1/3+1/5−1/7+…).[/math]