Окружность девяти точек
У каждого треугольника имеется, и притом единственная, окружность девяти точек. Это — окружность, проходящая через следующие три тройки точек, положение которых определено для треугольника (рис. 1): основания его высот [math]D_1,[/math] [math]D_2[/math] и [math]D_3,[/math] основания его медиан [math]D_4,[/math] [math]D_5[/math] и [math]D_6,[/math] середины [math]D_7,[/math] [math]D_8[/math] и [math]D_9[/math] отрезков прямых от точки пересечения его высот [math]Н[/math] до его вершин.
- Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения
Рис. 1.
<addc>r</addc>
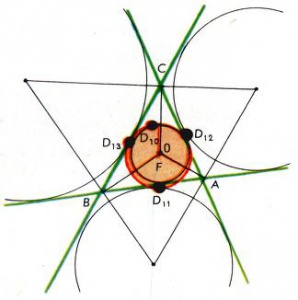
Эта окружность, найденная в XVIII в. великим ученым Л. Эйлером (поэтому её часто также называют окружностью Эйлера), была заново открыта в следующем столетии учителем провинциальной гимназии в Германии. Звали этого учителя Карл Фейербах (он был родным братом известного философа Людвига Фейербаха). Дополнительно К. Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого данного треугольника. Это — точки её касания с четырьмя окружностями специального вида (рис. 2). Одна из этих окружностей вписанная, остальные три — вневписанные. Они вписаны в углы треугольника и касаются внешним образом его сторон. Точки касания этих окружностей с окружностью девяти точек [math]D_{10},[/math] [math]D_{11},[/math] [math]D_{12}[/math] и [math]D_{13}[/math] называются точками Фейербаха. Таким образом, окружность девяти точек является в действительности окружностью тринадцати точек.
Окружность эту очень легко построить, если знать два её свойства. Во‑первых, центр окружности девяти точек лежит в середине отрезка, соединяющего центр описанной около треугольника окружности с точкой [math]H[/math] — его ортоцентром (точка пересечения его высот). Во‑вторых, её радиус для данного треугольника равен половине радиуса описанной около него окружности.