Маятник Максвелла

Прибор, который мы рекомендуем вам сделать, носит имя известного английского физика — маятник Максвелла. Несложный в изготовлении, он часто демонстрируется на лекциях по механике и позволяет выявить ряд интересных закономерностей движения твердого тела.

<addc>l</addc>

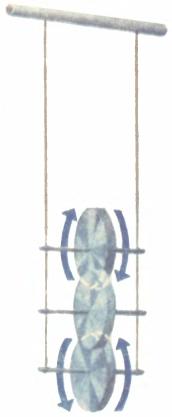
Посмотрите на рисунок такого маятника. Это диск, насаженный на ось, к которой привязаны две нити. Их верхние концы закреплены на перекладине. Закрутите нити вокруг оси — диск поднимается. Теперь отпустите маятник — и он начнет совершать периодическое движение: сначала диск опускается, нить раскручивается, диск вращается все быстрее; дойдя до нижней точки и продолжая по инерции вращаться, диск меняет направление своего движения и поднимается вверх. Так он совершает колебания, пока не остановится.

Несколько советов по изготовлению маятника: диск должен быть тяжелым ([math]m\gt 100[/math] г), большим ([math]d\gt 5[/math] см), ось — тонкой и легкой, нити — прочными и достаточно длинными ([math]0,5[/math] м). Лучше иметь набор дисков, меняемых на оси.

Легко выяснить, что период колебания маятника, т. е. полное время спуска и подъема, не зависит от массы диска, а зависит от его радиуса, причем зависимость эта почти прямо пропорциональная. Это указывает на то, что для описания движения маятника необходимо использовать такое понятие, как момент инерции [math]J[/math] (для диска [math]J=mr^2/2[/math]).

Точная формула для периода маятника Максвелла может быть получена путем довольно простых выкладок (см., например, журнал «Квант», 1981, №11).

[math]T=2\sqrt{\frac{2l}{g}\left( 1+\frac{J}{m{{r}^{2}}} \right)}[/math]

где [math]l[/math] — длина нити, [math]r[/math] — радиус оси диска, [math]J[/math] — момент инерции.

Эту формулу можно применять как для диска, так и для шара, соответственно изменив конструкцию маятника.