Гиперболические функции
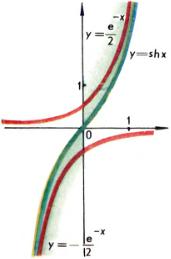
Функции, определяемые формулами sh x = (ex − e−x)/2, ch x = (ex + e−x)/2, называются соответственно гиперболическим синусом и гиперболическим косинусом. На рис. 1 и 2 приведены графики гиперболических функций. Гиперболический синус — возрастающая функция, нечетная, равная нулю при x = 0, положительная при x > 0 и отрицательная при x < 0. Гиперболический косинус — четная функция, в точке x = 0 принимает наименьшее значение. При неограниченном возрастании аргумента (x → +∞) обе эти функции очень быстро возрастают. С достаточной степенью точности их можно заменить при больших x просто показательной функцией ex/2
Нетрудно убедиться, что при любых x справедливо следующее равенство:
ch2x − sh2x = 1.
Гиперболические функции обладают многими свойствами, аналогичными свойствам тригонометрических функций, например справедливы следующие формулы:
sh (x + y) = sh x • ch y + ch x • sh y,
ch (x + y) = ch x • ch y + sh x • sh y,
sh 2x = 2 • sh x • ch x,
ch 2x = ch2 x + sh2 y.
Кроме функций sh x и ch x рассматриваются также гиперболические тангенс и котангенс, которые обозначаются th x и cth x; они определяются по формулам:
th x = sh x / ch x = (ex − e−x)/(ex + e−x);
cth x = (ex + e−x)/(ex − e−x).
Графики этих функций изображены на рис. 3.
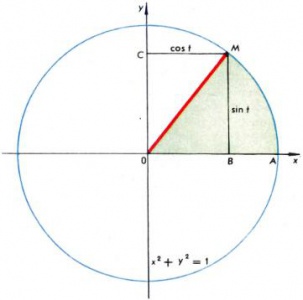
Название свое гиперболические функции получили потому, что они связаны с равнобочной гиперболой x2 − y2 = 1 так же, как функции синус и косинус связаны с единичной окружностью x2 + y2 = 1 (рис. 4 и 5). Если точка M лежит на единичной окружности, то её абсцисса и ордината соответственно равны x = cos t, y = sin t. Для точки M′, лежащей на гиперболе x2 − y2 = 1, абсциссу и ординату можно представить в виде x = ch t, y = sh t. Для окружности t равно углу AOM, но, кроме того, t также равно удвоенной площади сектора AOM. Последнее верно и для гиперболы, т. е. если t равно удвоенной площади гиперболического сектора AOM′, то координаты точки M′ равны x = ch t и y = sh t.
Гиперболические функции находят применение в электротехнике, строительной механике, сопротивлении материалов и др. С помощью гиперболических функций описывается, например, прогиб каната (цепи, проволоки, веревки); такая кривая называется цепной линией.