Вписанные и описанные фигуры
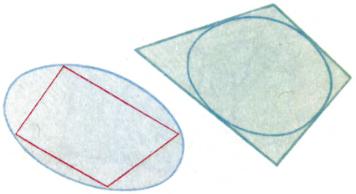
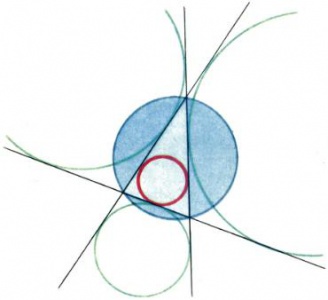
Многоугольник называется вписанным в выпуклую кривую, а кривая — описанной около многоугольника, если все вершины многоугольника лежат на кривой (рис. 1). Многоугольник называется описанным вокруг выпуклой кривой, а кривая — вписанной в многоугольник, если каждая его сторона касается кривой. Если же кривая касается всех прямых, на которых лежат стороны многоугольника, причем некоторых из них она касается в точках, не принадлежащих сторонам, то она называется вневписанной. В качестве кривой чаще всего рассматривается окружность. Так, например, всякий треугольник имеет одну описанную окружность, одну вписанную и три вневписанных (рис. 2).
Но уже не всякий четырехугольник имеет вписанную или описанную окружность. Описанная вокруг четырехугольника окружность существует лишь в том случае, если сумма его противоположных углов равна 180°. А для того чтобы в четырехугольник можно было вписать окружность, необходимо и достаточно, чтобы каждая сумма длин одной пары противоположных сторон была равна сумме длин второй пары сторон.
<addc>l</addc>
Вписанная и описанная окружности существуют у любого правильного многоугольника (рис. 3). Этот факт использовался еще в древности для нахождения отношения длины окружности к её радиусу.
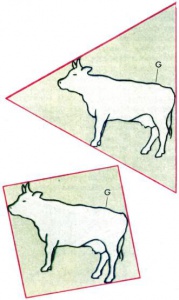
Нетрудно обнаружить тот факт, что если на плоскости задана замкнутая кривая G и равносторонний треугольник, то вокруг G всегда можно описать равносторонний треугольник со сторонами, параллельными сторонам данного (рис. 4). Менее очевидным является утверждение о том, что вокруг любой замкнутой кривой можно описать квадрат.
Вписанные и описанные фигуры рассматриваются и в пространстве.
В этом случае вместо многоугольника рассматривается многогранник, а вместо выпуклой линии — выпуклая поверхность, чаще всего сфера.
Сфера называется описанной около многогранника, а многогранник — вписанным в сферу, если все вершины многогранника лежат на сфере. Сфера называется вписанной в многогранник, а многогранник — описанным около сферы, если плоскости всех его граней касаются сферы.
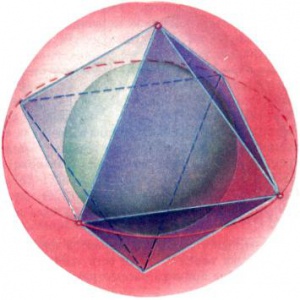
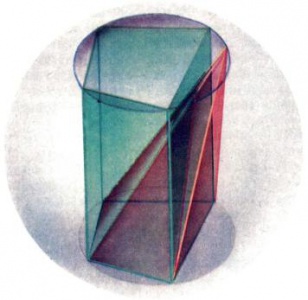
У правильных многогранников существуют описанные и вписанные сферы, поскольку вершины правильного многогранника равноудалены от его центра (рис. 5). Для того чтобы у других многогранников существовали описанная и вписанная сферы, требуются определенные условия. Например, около прямой призмы или пирамиды можно описать сферу, если можно описать окружность около её основания (рис. 6).
Иногда рассматривают конус, вписанный в сферу; сферу, вписанную в конус, цилиндр и т. п. (рис. 7).
На могильной плите Архимеда, как завещал ученый, был изображен цилиндр с вписанным шаром, а эпитафия говорила о величайшем открытии Архимеда — о том, что объемы этих тел относятся как 3:2. Когда римский оратор и общественный деятель Цицерон, живший в I в. до н. э., был в Сицилии, он еще видел этот заросший кустами и терновником памятник с шаром и цилиндром.