Ряд
Рядом в математике называется выражение вида
[math]{{a}_{1}}+{{a}_{2}}+{{a}_{3}}+\ldots ,[/math]
составленное из чисел [math]{{a}_{1}},{{a}_{2}},{{a}_{3}},\ldots ,[/math] которые называются членами ряда. Многоточие в конце (иногда шутят, что в нём‑то и заключена суть ряда) указывает, что выражение (1) не имеет последнего слагаемого, за каждым слагаемым всегда стоит следующее. Таким образом, ряд есть «бесконечная» сумма.
При сложении конечного числа слагаемых всегда получается определенный числовой результат, вычислить же сумму бесконечного числа слагаемых, вообще говоря, не сможет ни человек, ни компьютер, поскольку процесс сложения членов рада (по самому определению) никогда не кончается. Поэтому выражение (1) — это лишь некий математический символ, которому надлежит придать определенный смысл.
Рассмотрим конкретный ряд
[math]\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\ldots ,[/math]
каждый последующий член которого равен половине предыдущего.
Подсчитаем суммы одного, двух, трех, четырех, пяти его членов:
[math]\begin{matrix} \frac{1}{2} & {} & {} & {} & {} & =\frac{1}{2} \\ \frac{1}{2} & +\frac{1}{4} & {} & {} & {} & =\frac{3}{4} \\ \frac{1}{2} & +\frac{1}{4} & +\frac{1}{8} & {} & {} & =\frac{7}{8} \\ \frac{1}{2} & +\frac{1}{4} & +\frac{1}{8} & +\frac{1}{16} & {} & =\frac{15}{16} \\ \frac{1}{2} & +\frac{1}{4} & +\frac{1}{8} & +\frac{1}{16} & +\frac{1}{32} & =\frac{31}{32} \\ \end{matrix}[/math]
Нетрудно заметить, что значения этих сумм отличаются от [math]1[/math] на [math]1/2, 1/4, 1/8,[/math] [math]1/16, 1/32,[/math] т. е. при увеличении числа слагаемых мы получаем для их сумм хотя и различные числовые значения, однако все меньше и меньше отличающиеся от единицы. Число [math]1[/math] разумно назвать суммой ряда (2).
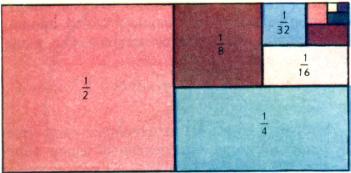
Подкрепим наши доводы еще следующим рассуждением. Прямоугольник площадью в [math]1[/math] квадратную единицу разобьем на два прямоугольника одинаковой площади (см. рис.). Один из получившихся прямоугольников вновь разобьем на два прямоугольника одинаковой площади. Продолжая мысленно этот процесс деления, получим прямоугольники, площади которых равны [math]1/2, 1/4, 1/8, …,[/math] [math]1/{{2}^{n}}, …[/math] квадратных единиц. Объединение всех этих прямоугольников дает исходный прямоугольник, значит, и сумма их площадей должна быть равна площади исходного:
[math]\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\ldots =1.[/math]
Приближенные суммы ряда (1)
[math]\begin{align} & {{S}_{1}}={{a}_{1}}, \\ & {{S}_{2}}={{a}_{1}}+{{a}_{2}}, \\ & {{S}_{3}}={{a}_{1}}+{{a}_{2}}+\ldots +{{a}_{n}} \\ \end{align}[/math]
называются частичными суммами. Если значения частичных сумм [math]{{S}_{n}}[/math] при неограниченном возрастании [math]n[/math] стремятся к некоторому числу [math]A[/math], то ряд называется сходящимся; число [math]А[/math] называют при этом суммой ряда и пишут:
[math]{{a}_{1}}+{{a}_{2}}+{{a}_{3}}+\ldots =A.[/math]
Таким образом, эта запись есть сокращенная форма следующего утверждения: при неограниченном возрастании [math]n[/math] значения [math]{{S}_{n}}[/math] сколь угодно мало отличаются от [math]A[/math], т. е. число [math]A[/math] есть предел последовательности [math]{{S}_{n}}[/math], что записывается так:
[math]\lim\limits_{x \to \infty} {{S}_{n}}=A.[/math]
Не для всякого ряда последовательность его частичных сумм стремится к определенному пределу. Например, для ряда
[math]1−1+1-1+…[/math]
частичные суммы [math]{{S}_{n}}[/math] принимают попеременно значения [math]1[/math] и [math]0[/math]:
[math]{{S}_{1}}=1,[/math] [math]{{S}_{2}}=1−1=0,[/math] [math]{{S}_{3}}=1,[/math] [math]{{S}_{4}}=0, …[/math]
и с ростом [math]n[/math], очевидно, не приближаются неограниченно к какому‑либо числу.
Ряд, у которого последовательность частичных сумм [math]{{S}_{n}}[/math] не имеет предела, называется расходящимся. Таков ряд (3). Расходящийся ряд не имеет суммы.
Примеры сходящихся рядов:
[math]\frac{3}{10}+\frac{3}{100}+\frac{3}{1000}+\frac{3}{10000}+\ldots ;[/math]
[math]1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\ldots ;[/math]
[math]\frac{1}{{{1}^{2}}}+\frac{1}{{{2}^{2}}}+\frac{1}{{{3}^{2}}}+\frac{1}{{{4}^{2}}}+\ldots .[/math]
Ряд (4) сходится к числу [math]1/3[/math] и дает представление этого числа бесконечной десятичной дробью: [math]1/3=0,333… .[/math] Суммы рядов (5) и (6) равны соответственно [math]π/4[/math] и [math]{{\pi }^{2}}/6[/math] и дают возможность приближенно вычислить число [math]π[/math] с любой степенью точности (если взять достаточно много членов ряда).
Для любого числа [math]x[/math], удовлетворяющего условию [math]−1 \lt x \lt 1[/math], сходящимся будет геометрический ряд
[math]1+x+{{x}^{2}}+{{x}^{3}}+{{x}^{4}}+\ldots [/math]
(его члены образуют геометрическую прогрессию со знаменателем [math]x[/math]). Сумма его первых [math]n[/math] членов, т. е. частичная сумма [math]{{S}_{n}}[/math], равна
[math]{{S}_{n}}=\frac{1-{{x}^{n}}}{1-x}[/math]
и в случае [math]−1 \lt x \lt 1[/math] при [math]n→∞[/math] стремится к [math]1/(1−х).[/math] Поэтому при [math]−1\lt х\lt 1[/math] можно написать:
[math]1+x+{{x}^{2}}+{{x}^{3}}+\ldots =[/math][math]1/(1-x).[/math]
Геометрический ряд исторически был первым бесконечным рядом, для которого была определена его сумма. Архимед (III в. до н. э.) для вычисления площади параболического сегмента (т. е. фигуры, ограниченной прямой и параболой) применил суммирование бесконечной геометрической прогрессии со знаменателем [math]1/4[/math].
Интересно, что после Архимеда вплоть до XVI в. математика рядами не занималась, ряды вошли в математику лишь тогда, когда началось изучение изменяющихся процессов. Математики занялись вычислением сумм рядов (например, для ряда (5) сумму нашел Г. Лейбниц, а для ряда (6) — Л. Эйлер), хотя понятие сходимости ряда точно установлено ещё не было. Считалось, что любой ряд имеет сумму и с рядами можно производить те же арифметические действия, что и с многочленами: складывать, умножать, переставлять слагаемые и т. п. Иногда это приводило к фантастическим результатам, например, получали, что сумма ряда [math]1−1+1−1+…[/math] может быть равна и [math]0[/math], и [math]1[/math], и даже [math]1/2[/math]. Рассуждения были примерно такие: [math]1−1+1−1+…=[/math] [math](1−1)+(1−1)+…=0[/math] или [math]1−1+1−1+1−…=[/math] [math]1−(1−1)−(1−1)−…=1,[/math] а результат [math]1/2[/math] получался следующим образом: если [math]S=1−1+1−1+1−…,[/math] то из равенства [math]1−1+1−1+…=[/math] [math]1−(1−1+1−1+…)[/math] следует [math]S=1−S,[/math] откуда [math]S=1/2.[/math] Позже сходящимися рядами стали считать лишь те ряды, у которых [math]n[/math]‑й член [math]{{a}_{n}}[/math] при неограниченном возрастании [math]n[/math] стремится к нулю. Если ряд сходится, то предел [math]{{a}_{n}}[/math] действительно равен нулю, так как [math]{{a}_{n}}={{S}_{n}}-{{S}_{n-1}}[/math] и с возрастанием [math]n[/math] эта разность стремится к нулю. Однако нашлись ряды, у которых [math]{{a}_{n}}[/math] стремится к нулю, а последовательность частичных сумм не имеет конечного предела. Таков, например, гармонический ряд
[math]1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\ldots .[/math]
Четкое определение сходимости ряда, основанное на понятии предела последовательности частичных сумм, появилось лишь в начале XIX в. Тогда же началось систематическое изучение рядов.
Некоторые числовые ряды обладают тем свойством, что их сумма не меняется при перестановке членов, например абсолютно сходящиеся ряды. Ряд (1) называется абсолютно сходящимся, если сходится ряд
[math]|{{a}_{1}}|+|{{a}_{2}}|+|{{a}_{3}}|+\ldots [/math]
из абсолютных величин его членов. Таковы ряды (2), (4) и (6), а ряд (5) не является абсолютно сходящимся. Абсолютно сходящиеся ряды можно складывать, вычитать, умножать и делить по тем же правилам, что и конечные суммы.
Особое значение имеет степенной ряд, т. е. ряд вида
[math]{{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+{{a}_{3}}{{x}^{3}}+\ldots .[/math]
Для одних значений [math]x[/math] получающийся из (8) числовой ряд может сходиться, для других — расходиться (например, геометрический ряд (7) сходится при любом [math]x[/math], удовлетворяющем условию [math]−1 \lt x \lt 1[/math], а при [math]x=−1[/math] дает расходящийся ряд [math]1−1+1−1+…[/math]).
Множество всех значений [math]x[/math], для которых ряд (8) сходится, называется множеством сходимости этого ряда. На множестве сходимости сумма ряда (8) зависит от [math]x[/math] и является функцией аргумента [math]x[/math]. Если
[math]{{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+[/math] [math]{{a}_{3}}{{x}^{3}}+\ldots .=f(x),[/math]
то левая часть равенства представляет собой разложение функции [math]f(x)[/math] в бесконечный степенной ряд. Например, формула (7) дает разложение функции [math]1/(1−x)[/math] при [math]−1 \lt x \lt 1[/math] в бесконечный степенной ряд.
Идея представления функций степенными рядами принадлежит И. Ньютону, он нашел разложения многих функций, например:
[math]\sin x=x-\frac{{{x}^{3}}}{1\cdot 2\cdot 3}+[/math] [math]\frac{{{x}^{5}}}{1\cdot 2\cdot 3\cdot 4\cdot 5}-[/math] [math]\frac{{{x}^{7}}}{1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7}+\ldots [/math]
где [math]x[/math] — радианная мера угла, этот ряд сходится (и к тому же абсолютно) для любого [math]x[/math]. Если в разложении (9) функции [math]f(x)[/math] в степенной ряд ограничиться несколькими первыми членами, то мы получим приближенное представление функции: оно тем точнее, чем больше взято членов ряда (слагаемых). Например, приближенная формула
[math]\sin x\approx x-\frac{{{x}^{3}}}{6},[/math]
правая часть которой — первые два члена формулы (10), дает значения [math]\sin x[/math] с ошибкой, меньшей [math]0,0005[/math], при всех [math]0 \lt x \lt 0,59[/math], что в градусной мере соответствует углам [math]0°\lt x \lt 32°38′[/math]. С той же точностью до [math]0,0005[/math] можно считать [math]\sin x\approx x[/math] при всех положительных [math]x[/math], меньших [math]6°33′[/math].
Существуют различные способы представления функций бесконечными рядами, например, при рассмотрении периодических процессов используются тригонометрические ряды, т. е. ряды вида
[math]{{a}_{0}}+{{a}_{1}}\sin x+{{b}_{1}}\cos x+[/math] [math]{{a}_{2}}\sin 2x+{{b}_{2}}\cos 2x+\ldots .[/math]
<addc>G</addc>
Заметим, что все рассмотренные ряды имели ясный и вполне определенный закон образования их членов. Обычно же ряд задается формулой [math]n[/math]‑го члена ряда ([math]{{a}_{n}}[/math]), его называют общим членом ряда. Из этой формулы подстановкой вместо [math]n[/math] определенного числа — номера члена ряда — находят слагаемое, имеющее этот номер. Например, общий член ряда (2) имеет вид [math]{{a}_{n}}=1/{{2}^{n}},[/math] и легко находятся [math]a_1=1/2,[/math] [math]{{a}_{2}}=1/{{2}^{2}}=1/4,[/math] [math]{{a}_{3}}=1/{{2}^{3}}=1/8.[/math] Для ряда (3) общий член выражается так: [math]{{a}_{n}}={{(-1)}^{n-1}}.[/math] Для краткой записи суммы употребляется символ [math]∑[/math] (греческая буква «сигма», начальная буква слова «сумма»). Символ [math]\sum\limits_{n=1}^{N}[/math] (читается «сумма по [math]n[/math] от [math]1[/math] до [math]N[/math]») означает сумму всех слагаемых, получаемых, когда [math]n[/math] последовательно пробегает значения от [math]1[/math] до [math]N[/math], например:
[math]\sum\limits_{n=1}^{5}{\frac{1}{{{2}^{n}}}}=\frac{1}{2}+\frac{1}{{{2}^{2}}}+[/math] [math]\frac{1}{{{2}^{3}}}+\frac{1}{{{2}^{4}}}+\frac{1}{{{2}^{5}}},[/math]
[math]\sum\limits_{n=1}^{N}{\frac{1}{{{2}^{n}}}}=\frac{1}{2}+\frac{1}{{{2}^{2}}}+[/math] [math]\frac{1}{{{2}^{3}}}+\ldots +\frac{1}{{{2}^{N}}}.[/math]
Для обозначения всего ряда верхний индекс заменяется на символ бесконечности [math]∞[/math]:
[math]{{a}_{1}}+{{a}_{2}}+{{a}_{3}}+\ldots +[/math] [math]{{a}_{n}}+\ldots =\sum\limits_{n=1}^{\infty }{{{a}_{n}}}.[/math]
Таким образом, можно записать:
[math]\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+[/math] [math]\ldots =\sum\limits_{n=1}^{N}{\frac{1}{{{2}^{n}}}},[/math]
[math]1-1+1-1+\ldots =[/math] [math]\sum\limits_{n=1}^{\infty }{{{(-1)}^{n-1}}.}[/math]