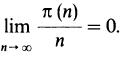Простое число
Натуральные числа, отличные от единицы, подразделяют на простые и составные. Простым называется такое натуральное число, делителями которого являются только оно само и единица. Остальные числа называются составными. Евклид определял простые числа так: «Простое число есть измеряемое только единицей, составное число есть измеряемое некоторым числом». Примеры простых чисел: 2, 5, 37, 1987. Числа же 4, 6, 162, 2553 составные. Число 1 не относят ни к простым, ни к составным. Простых чисел, так же как и составных, бесконечно много.
Каждое составное натуральное число можно разложить на простые множители. Например: 4 = 2•2, 6 = 2•3, 162 = 2•3•3•3•3, 2553 = 3•23•37. Можно сказать, что простые числа представляют собой как бы элементарные кирпичики, из которых строятся остальные числа.
«Основная теорема арифметики» утверждает, что любые два разложения данного натурального числа на простые множители одинаковы, если не обращать внимание на порядок следования сомножителей.
Для того чтобы доказать, что данное натуральное число N простое, достаточно установить, что оно не делится ни на одно из чисел от 2 до √N. Если же N делится на одно из таких чисел, то N составное.
Более удобный способ «отсеивания» составных чисел основан на следующем наблюдении. Если выписать подряд последовательные натуральные числа, то, зачеркивая каждое второе число из следующих за числом 2, мы отсеем все числа, кратные числу 2; зачеркивая каждое третье число из следующих за числом 3, мы отсеем все числа, кратные 3, и, вообще, какое бы натуральное число k мы ни взяли, зачеркивая каждое k‑е число из стоящих за k, мы отсеем все числа, кратные k. Поэтому если нам нужно отыскать все простые числа, не превосходящие данного числа N, то выпишем подряд все числа от 2 до N. Отметим число 2 как первое простое. Затем по способу «отсеивания» отбросим все числа, кратные 2; первое невычеркнутое число — это следующее простое число 3. Отбросим все числа, кратные 3; первое невычеркнутое число — это следующее простое число 5 и т. д. Будем продолжать этот процесс до тех пор, пока не доберемся до простого числа, которое больше √N. Все оставшиеся невычеркнутыми числа будут простыми.
Такой способ отыскания простых чисел был известен еще греческому математику Эратосфену, жившему в III в. до н. э. Во времена Эратосфена писали на восковых дощечках, а вместо того чтобы числа вычеркивать, дощечку в нужном месте прокалывали. Отсюда и название способа — «решето Эратосфена».
В разные времена математики искали формулу, которая при различных значениях входящих в нее переменных давала бы простые числа. Так, Л. Эйлер указал многочлен n2 − n + 41, значения которого при n = 0, 1, 2, …, 40 — простые числа. Однако легко доказать, что нет многочлена от одной переменной, который при всех целых её значениях принимает простые значения. П. Ферма высказал предположение, что все числа вида 22k + 1 простые (при k = 0, 1, 2, 3, 4 это числа 3, 5, 17, 257, 65537). Однако Л. Эйлер опроверг это предположение, доказав, что при k = 5 число 22k + 1 составное. Все же известны формулы, принимающие при всех целых значениях переменных простые значения. Так, математик Ю. В. Матиясевич доказал, что существует многочлен от нескольких переменных, который принимает все простые значения по одному разу, причем все положительные его значения — простые числа.
Издавна математиков интересовал вопрос о распределении простых чисел в натуральном ряду.
Рассуждение Евклида, доказывающее бесконечность числа простых чисел в натуральном ряду (см. Алгоритм Евклида), применимо и для доказательства бесконечности числа простых чисел некоторого специального вида, например простых чисел вида 4n − 1. Чуть видоизменяя это рассуждение, можно получить доказательство бесконечности количества простых чисел вида 4n + 1, 6n + 1 и некоторых других.
В 1837 г. немецкому математику Л. Дирихле удалось доказать, что в любой арифметической прогрессии, первый член и разность которой взаимно просты, есть бесконечно много простых чисел. В доказательстве Дирихле были использованы новые для теории чисел методы (функции комплексного переменного, ряды), открывшие совершенно новые пути для её развития. О простых числах более сложного вида известно мало. Так, до сих пор неизвестно, конечно или бесконечно число простых чисел вида n2 + 1 или же простых чисел вида 2n − 1 (эти последние называются простыми числами Мерсенна). Наибольшее из известных простых чисел является простым числом Мерсенна и равно 2132049 − 1.
Вопрос о том, как часто простые числа встречаются в натуральном ряду и как они распределены среди натуральных чисел, оказался очень сложным. Изучение таблиц простых чисел показывает, что в натуральном ряду есть участки, где простые числа располагаются гуще. Есть даже числа, которые находятся совсем близко друг от друга, как, например, 2 и 3, 3 и 5, 191 и 193, 2711 и 2713. Такие пары чисел называются близнецами. До сих пор неизвестно, конечно или бесконечно число пар близнецов. Но есть и сколь угодно длинные отрезки натурального ряда, в которых нет ни одного простого числа. Например, среди последовательных чисел k! + 2, k! + 3, ..., k! + k нет ни одного простого.
Важными характеристиками расположения простых чисел в натуральном ряду служат величины: π(n) — число простых чисел, не превосходящих n, и отношение π(n)/n — средняя плотность простых чисел среди первых n натуральных. Изучение таблиц простых чисел показало, что, двигаясь по натуральному ряду, мы будем встречать простые числа в среднем все реже. Эйлер обосновал это наблюдение, доказав, что
Отсюда, в частности, следует, что простые числа в среднем располагаются реже, чем члены какой угодно арифметической прогрессии. Можно доказать, что простые числа располагаются все же гуще квадратов натуральных чисел.
Но все эти результаты очень мало говорят о самом числе π(n). Математикам хотелось получить для π(n) какую-нибудь достаточно простую приближенную формулу. Первая гипотеза о величине π(n) была сделана независимо французским математиком А. Лежандром и К. Гауссом около 1800 г. Она заключалась в том, что π(n) ≈ n/ln n. Однако доказать это утверждение удалось лишь 100 лет спустя.
Большой вклад в разработку этого доказательства внес П. Л. Чебышев, а окончательный результат был получен в 1896 г. французским математиком Ж. Адамаром и бельгийским математиком Ш. Валле-Пуссеном. Кроме того, в 1852 г. Чебышев доказал предположение французского математика Ж. Бертрана о том, что для любого натурального числа n между числами n и 2n всегда есть простое число.