Сфера и шар
Точки пространства, удаленные от данной точки [math]O[/math] на данное расстояние [math]R[/math], образуют сферу с центром [math]O[/math] и радиусом [math]R[/math]. Сфера ограничивает шар, состоящий из точек, удаленных от [math]O[/math] на расстояние, не большее [math]R[/math]. Эти геометрические объекты, так же как окружность и круг, рассматривали ещё в глубокой древности. Открытие шарообразности Земли, появление представлений о небесной сфере дали толчок к развитию специальной науки — сферики, изучающей расположенные на сфере фигуры (см. Сферическая геометрия). Рассмотрим основные вопросы классической стереометрии: взаимное расположение шара (сферы) и других пространственных фигур, измерение объема шара и его частей, а также площади сферы и её частей.
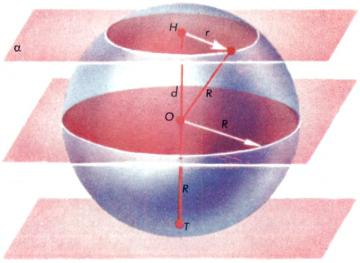
Прежде всего, плоскость [math]α[/math], проведенная на расстоянии [math]d\lt R[/math] от центра [math]O[/math] шара радиуса [math]R[/math], в пересечении с шаром дает круг радиуса [math]r=\sqrt{{{R}^{2}}-{{d}^{2}}}[/math] с центром в точке [math]H[/math] — основании перпендикуляра, проведенного из [math]O[/math] к [math]α[/math] (рис. 1). Если плоскость [math]α[/math] отстоит от центра [math]O[/math] на расстояние [math]d=R[/math], то [math]α[/math] имеет с шаром (и сферой) единственную общую точку [math]T[/math]. Такие плоскости называются касательными к шару (сфере); они характеризуются тем, что перпендикулярны радиусу [math]OT[/math], проведенному в точку касания.
<addc>G</addc>
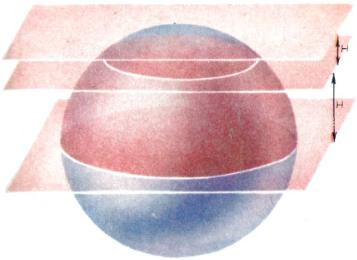
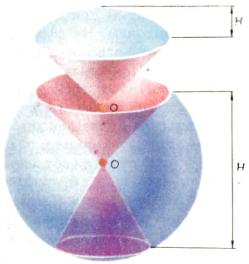
Круговое сечение шара делит его на два шаровых сегмента, а сферу — на две сегментные поверхности. Часть шара, ограниченная двумя параллельными круговыми сечениями и лежащим между ними сферическим поясом (или зоной), называется шаровой зоной (рис. 2). Радиусы, проведенные от центра шара к точкам сферы, принадлежащим одной сегментной поверхности или сферическому поясу, образуют шаровой сектор — он может быть ограничен сферическим сегментом или зоной и одной или двумя коническими поверхностями (рис. 3). Высота шаровой или сферической зоны — это расстояние между плоскостями сечений; высота шарового сегмента или сегментной поверхности определяется как расстояние от плоскости сечения до параллельной ей плоскости, касательной к этому сегменту (рис. 2). Высоту шарового сектора определяют как высоту соответствующей сегментной поверхности или сферического пояса (рис. 3).
Еще в Древней Греции умели вычислять объемы шаровых секторов и площади сферических зон или сегментов по формулам:
[math]{{V}_{С}}=\frac{2}{3}\pi {{R}^{2}}H,[/math] [math]{{S}_{З}}=2\pi RH,[/math]
где [math]π[/math], как обычно, — отношение длины окружности к её диаметру. Рассматривая шар и сферу как частные случаи шарового сектора и сферической зоны — с высотами [math]H=2R[/math], — мы получаем формулы для объема шара и площади сферы:
[math]{{V}_{Ш}}=\frac{4}{3}\pi {{R}^{3}},[/math] [math]{{S}_{СФ}}=4\pi {{R}^{2}}.[/math]
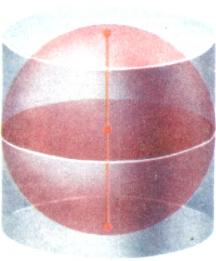
Архимед интерпретировал эти формулы так: объем и поверхность шара составляют [math]2/3[/math] от объема и полной поверхности описанного около шара цилиндра (рис. 4; по желанию Архимеда такой чертеж был изображен на его гробнице).