Степенная функция
Степенная функция — функция вида [math]y=x^α[/math], где [math]α[/math] — заданное число, называемое показателем степени. Иногда степенной функцией называется функция несколько более общего вида [math]y=ax^α[/math].
<addc>l</addc>
Многие функциональные зависимости выражаются через степенную функцию. Например, объем куба [math]V[/math] есть степенная функция от [math]x[/math] (длины его ребра): [math]V=x^3[/math]; период [math]T[/math] колебаний математического маятника пропорционален длине маятника [math]x[/math] в степени [math]1/2[/math], а именно [math]T=2π\sqrt{x/g}[/math]. Если газ расширяется или сжимается без теплообмена с окружающей средой, то его давление [math]P[/math] и объем [math]V[/math] связаны формулой [math]V⋅P^k=C[/math] (для воздуха, например, [math]k=−1,4[/math]). Заметим, что в двух последних случаях показатель не является целым числом.
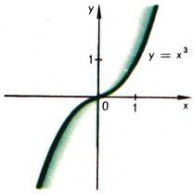
При любом показателе степени [math]α[/math] показательная функция [math]y=x^α[/math] определена во всяком случае на положительной полуоси. Свойства степенной функции различны в зависимости от значения показателя степени. Если [math]α[/math] — натуральное число [math](α=n)[/math], то функция [math]y=x^n[/math] определена на всей числовой оси, обращается в нуль при [math]x=0[/math], четная при четном [math]n[/math] и нечетная при [math]n[/math] нечетном, неограниченно возрастает при безграничном возрастании аргумента [math]x[/math]. На рис. [math]1[/math] и [math]2[/math] приведены графики типичных степенных функций с целым положительным показателем: [math]y=x^3[/math] (кубическая парабола) и [math]y=x^4[/math] (парабола четвертой степени). При [math]n=1[/math] степенная функция [math]y=x[/math] является линейной функцией, при [math]n=2[/math] — квадратичной функцией [math]y=x^2[/math].
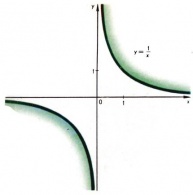
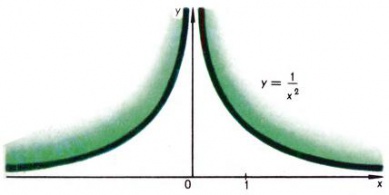
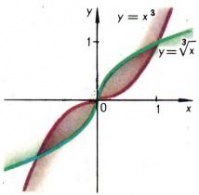
Если [math]α[/math] — отрицательное целое число [math](α=−n)[/math], то степенная функция определяется равенством [math]y=1/x^n[/math]. Она определена при всех отличных от нуля [math]x[/math]. Её график состоит из двух частей (ветвей), имеющих асимптотами оси координат, к которым эти кривые неограниченно приближаются. Типичные представители — функции [math]y=1/x[/math] и [math]y=1/x^3[/math], их графики даны на рис. [math]3[/math] и [math]4[/math]. При [math]α=0[/math] по определению [math]x^0=1[/math]. Если [math]α=1/n[/math], то функция [math]y=x^{1/n}[/math] (обозначается также [math]y=\sqrt[n]{x})[/math] определяется как обратная функция для функции [math]y=x^n[/math]. При четном [math]n[/math] функция определена лишь для [math]x≥0[/math], а при нечетном [math]n[/math] — на всей оси. Графики таких функций [math]y=\sqrt{x}[/math] и [math]y=\sqrt[3]{x}[/math] изображены на рис. [math]5[/math] и [math]6[/math].
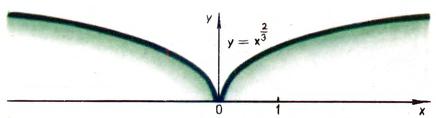
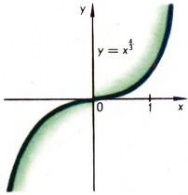
Для рационального показателя [math]α=p/q[/math] ([math]p/q[/math] — несократимая дробь) степенная функция определяется формулой
[math]y=x^{p/q}=(x^{1/q})^p[/math].
Графики типичных степенных функций с рациональным показателем приведены на рис. [math]7, 8, 9[/math].