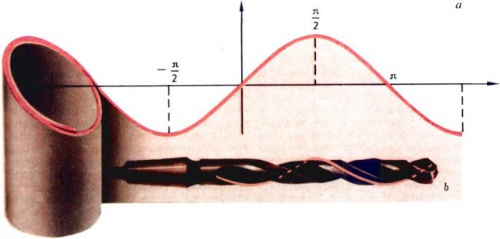
Синусоида
Синусоида — волнообразная плоская кривая, которая является графиком тригонометрической функции [math]y=\sin x[/math] в прямоугольной системе координат. Если рулончик бумаги разрезать наискось и развернуть его, то край бумаги окажется разрезанным по синусоиде (рис. 1,а). Любопытно, что проекция на плоскость винтовой линии также будет синусоидой (рис. 1,б).
Длина «волны» синусоиды равна [math]2π[/math]. Это объясняется тем, что значение функции [math]y=\sin x[/math] при любом [math]х[/math] совпадает с её значением при [math]x+2π[/math] (т. е. период функции равен [math]2π[/math]).
Синусоида пересекает ось [math]Ox[/math] в точках [math]πk[/math], которые являются точками перегиба; в точках [math]π/2+2πk[/math] синусоида имеет максимум, а в точках [math]−π/2+2πk[/math] — минимум ([math]k = 0, ±1, ±2, …[/math]).
Часто синусоидой называют кривую, которая является графиком функции вида [math]y=A\sin (\omega x+\varphi )+b[/math]. График этой функции получается из синусоиды [math]y=\sin x[/math] сдвигом по оси [math]Ox[/math] на [math]−φ[/math], растяжением (сжатием) в [math]ω[/math] раз по оси [math]Ox[/math], растяжением (сжатием) в [math]A[/math] раз по оси [math]Oy[/math] и сдвигом по оси [math]Oy[/math] на [math]b[/math]. Число [math]A[/math] называется амплитудой (или размахом), [math]ω[/math] — круговой частотой, [math]φ[/math] — начальной фазой колебания.
График функции [math]y=\cos x[/math] получается из синусоиды сдвигом влево на [math]π/2[/math] и тоже называется синусоидой (реже косинусоидой).
Изменение какой‑либо величины по закону синуса называется гармоническим колебанием. Примеры таких колебаний: колебания маятника, колебания напряжения в электрической сети, изменение тока и напряжения в колебательном контуре и др.
Еще один пример синусоидальных колебаний — звук (гармонические колебания воздуха). Однако редко удается услышать чистый звук — звук, соответствующий колебанию [math]y=A\sin \omega t[/math]. В большинстве случаев мы слышим ряд других звуков (обертоны), соответствующих колебаниям с меньшей амплитудой. Эти звуки музыкальных инструментов дают основному тону специфическую окраску — тембр.