Развёртка
Допустим, что многогранник — многогранную поверхность — после проведения разрезов по нескольким ребрам удается развернуть на плоскость. В результате получается развертка многогранника. Развертка представляет собой плоский многоугольник, составленный из меньших многоугольников — граней исходного многогранника. Так, на рис. 1 изображены развертки всех пяти видов правильных многогранников. По ним легко восстановить, склеить соответствующие многогранники; обычно на развертках указывают, какие именно пары сторон развертки нужно склеивать для получения исходного многогранника.
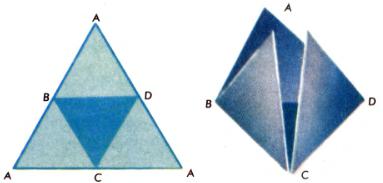
Один и тот же многогранник может иметь несколько разных разверток. Например, правильный тетраэдр имеет и треугольную развертку, которая даже более удобна для склейки тетраэдра: достаточно согнуть три угловых треугольника (рис. 2). Аналогичная развертка произвольного тетраэдра представляет собой в общем случае шестиугольник с попарно равными соседними сторонами (рис. 3).
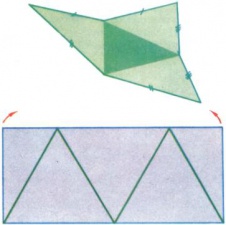
Развертки (или части разверток) применяют при изготовлении моделей различных многогранников. Пример — склейка «треугольных» (правильнее говорить «тетраэдрических») молочных пакетов. Эти пакеты не являются правильными тетраэдрами: правильные тетраэдры плохо укладываются в молочные корзины. Молочные пакеты представляют собой равногранные тетраэдры с четырьмя ребрами примерно по 17 см и двумя ребрами по 13 см. Внимательно рассмотрев пакет, вы увидите, что он склеен из… прямоугольника, получающегося при разрезании тетраэдра по двум меньшим ребрам и большей высоте одной из граней. Легко представить обратную процедуру: как показано на рис. 4, сначала прямоугольник склеивается в цилиндр (точнее, в боковую поверхность цилиндра), а потом вдоль взаимно перпендикулярных диаметров оснований в тетраэдрический пакет. Конечно, технологически это осуществить проще, чем склейку пакета из треугольника, — не потребуется даже никаких клапанов для склейки.
<addc>G</addc>
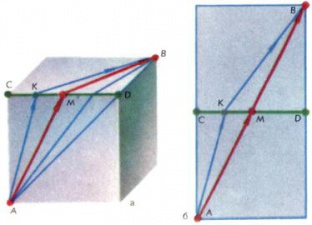
Развертки помогают решать задачи на отыскание кратчайшего пути (по поверхности фигуры) из одной точки в другую. Например, чтобы из всех путей вида AKB, ведущих по поверхности куба из вершины A в противолежащую вершину B (рис. 5, а), выбрать кратчайший, достаточно развернуть две соседние грани и соединить точки A и B отрезком прямой (рис. 5, б). Кратчайший путь будет проходить через середину M ребра CD (всего таких путей будет 6 — по числу разделяющих точки A и B ребер куба). Обратите внимание: точно так же решается и задача о кратчайшем «перевале» через ребро любого двугранного угла (рис. 6).
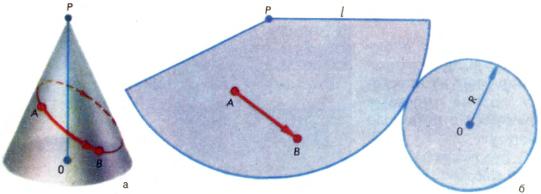
Рассматривая молочный пакет, мы видели, что цилиндрическую поверхность тоже можно развернуть на плоскость. Это верно и для поверхности конуса: разрезав её по окружности основания и по одной из образующих, после разворачивания мы получим (касающиеся друг друга) круг и круговой сектор (рис. 7, а, б). Если кривая на поверхности не пересекает линии разреза, то её длина при разворачивании не меняется. Поэтому и в случае цилиндра и конуса развертку можно применить для отыскания кратчайшего пути из точки A в точку B, идущего по боковой поверхности конуса или цилиндра. Конечно, при этом следует позаботиться о выборе линии, по которой делать разрез, иначе можно получить не самый короткий путь, а лишь более короткий по сравнению с ближайшими путями (пунктир на рис. 7, а).
Развертки цилиндра и конуса можно использовать и для вычисления площадей их боковых поверхностей ([math]2πRH[/math] — для цилиндра и [math]πRl[/math] — для конуса). Однако этот метод определения площадей далек от универсальности, ибо большинство искривленных поверхностей нельзя развернуть на плоскость с сохранением длин и площадей. С этим, в частности, связаны трудности при изготовлении покрышек для мячей.