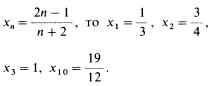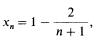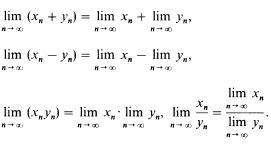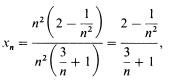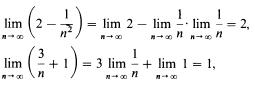Последовательность
Последовательность — одно из основных понятий математики. Последовательность может быть составлена из чисел, точек, функций, векторов и т.д. Последовательность считается заданной, если указан закон, по которому каждому натуральному числу n ставится в соответствие элемент xn некоторого множества. Последовательность записывается в виде x1, x2, …, xn, или кратко (xn). Элементы x1, x2, …, xn называются членами последовательности, x1 — первым, x2 — вторым, xn — общим (n-м) членом последовательности.
Наиболее часто рассматривают числовые последовательности, т. е. последовательности, члены которых — числа. Аналитический способ — самый простой способ задания числовой последовательности. Это делают с помощью формулы, выражающей n-й член последовательности х1 через его номер n. Например, если
Другой способ — рекуррентный (от латинского слова recurrens — «возвращающийся»), когда задают несколько первых членов последовательности и правило, позволяющее вычислять каждый следующий член через предыдущие. Например:
Примеры числовых последовательностей — арифметическая прогрессия и геометрическая прогрессия.
Интересно проследить поведение членов последовательности при неограниченном возрастании номера n (то, что n неограниченно возрастает, записывается в виде n → ∞ и читается: «n стремится к бесконечности»).
Рассмотрим последовательность с общим членом xn = 1/n: x1 = 1, x2 = 1/2; x3 = 1/3, …, x100 = 1/100, …. Все члены этой последовательности отличны от нуля, но чем больше n, тем меньше xn отличается от нуля. Члены этой последовательности при неограниченном возрастании n стремятся к нулю. Говорят, что число нуль есть предел этой последовательности.
Другой пример: xn = (−1)n/n — определяет последовательность
Члены этой последовательности также стремятся к нулю, но они то больше нуля, то меньше нуля - своего предела.
Рассмотрим еще пример: xn = (n − 1)/(n + 1). Если представить xn в виде
то станет понятно, что эта последовательность стремится к единице.
Дадим определение предела последовательности. Число a называется пределом последовательности (xn), если для любого положительного числа ε можно указать такой номер N, что при всех n > N выполняется неравенство |xn − a| < ε.
Если a есть предел последовательности (xn), то пишут xn → a, или a = limn→∞ xn (lim — три первые буквы латинского слова limes — «предел»).
Это определение станет понятнее, если ему придать геометрический смысл. Заключим число a в интервал (a − ε, a + ε) (см. рис.). Число а есть предел последовательности (xn), если независимо от малости интервала (a − ε, a + ε) все члены последовательности с номерами, бо́льшими некоторого N, будут лежать в этом интервале. Иными словами, вне любого интервала (a − ε, a + ε) может находиться лишь конечное число членов последовательности.
Для рассмотренной последовательности xn = (−1)n/n в ε-окрестность точки нуль при ε = 1/10 попадают все члены последовательности, кроме первых десяти, а при ε = 1/100 — все члены последовательности, кроме первых ста.
Последовательность, имеющая предел, называется сходящейся, а не имеющая предела — расходящейся. Вот пример расходящейся последовательности: xn = (−1)n. Ее члены попеременно равны +1 и −1 и не стремятся ни к какому пределу.
Если последовательность сходится, то она ограничена, т. е. существуют такие числа c и d, что все члены последовательности удовлетворяют условию c ≤ xn ≤ d. Отсюда следует, что все неограниченные последовательности расходящиеся. Таковы последовательности:
Стремящаяся к нулю последовательность называется бесконечно малой. Понятие бесконечно малой может быть положено в основу общего определения предела последовательности, так как предел последовательности (xn) равен a тогда, и только тогда, когда xn представимо в виде суммы xn = a + αn, где αn бесконечно малая.
Рассмотренные последовательности (1/n), ((−1)n/n) являются бесконечно малыми. Последовательность (n − 1)/(n + 1), как следует из (2), отличается от 1 на бесконечно малую 2/(n + 1), и потому предел этой последовательности равен 1.
Большое значение в математическом анализе имеет также понятие бесконечно большой последовательности. Последовательность (xn) называется бесконечно большой, если последовательность (1/xn) бесконечно малая. Бесконечно большую последовательность (xn) записывают в виде xn → ∞, или limn→∞ xn = ∞, и говорят, что она «стремится к бесконечности». Вот примеры бесконечно больших последовательностей:
(n2), (2n), (√(n + 1)), (n - n2).
Подчеркнем, что бесконечно большая последовательность не имеет предела.
Рассмотрим последовательности (xn) и (yn). Можно определить последовательности с общими членами xn + yn, xn − yn, xnyn и (если yn ≠ 0) xn/yn. Справедлива следующая теорема, которую часто называют теоремой об арифметических действиях с пределами: если последовательности (xn) и (yn) сходящиеся, то сходятся также последовательности (xn + yn), (xn − yn), (xnyn), (xn/yn) и имеют место равенства:
В последнем случае необходимо потребовать, кроме того, чтобы все члены последовательности (yn) были отличны от нуля, еще и чтобы выполнялось условие limn→∞ yn ≠ 0.
Применяя эту теорему, можно находить многие пределы. Найдем, например, предел последовательности с общим членом
Представив xn в виде
установим, что предел числителя и знаменателя существует:
поэтому получим:
limn→∞ xn = 2/1 =2.
Важный класс последовательностей — монотонные последовательности. Так называют последовательности возрастающие (xn+1 > xn при любом n), убывающие (xn+1 < xn), неубывающие (xn+1 ≥ xn) и невозрастающие (xn+1 ≤ xn). Последовательность (n − 1 )/(n + 1) возрастающая, последовательность (1/n) убывающая. Можно доказать, что рекуррентно заданная последовательность (1) монотонно возрастает.
<addc>G</addc>
Представим себе, что последовательность (xn) не убывает, т. е. выполняются неравенства
x1 ≤ x2 ≤ x3 ≤ … ≤ xn ≤ xn+1 ≤ …,
и пусть, кроме того, эта последовательность ограничена сверху, т. е. все xn не превосходят некоторого числа d. Каждый член такой последовательности больше предыдущего или равен ему, но все они не превосходят d. Вполне очевидно, что эта последовательность стремится к некоторому числу, которое либо меньше d, либо равно d. В курсе математического анализа доказывается теорема, что неубывающая и ограниченная сверху последовательность имеет предел (аналогичное утверждение справедливо для невозрастающей и ограниченной снизу последовательности). Эта замечательная теорема дает достаточные условия существования предела. Из нее, например, следует, что последовательность площадей правильных n-угольников, вписанных в окружность единичного радиуса, имеет предел, так как является монотонно возрастающей и ограниченной сверху. Предел этой последовательности обозначается π.
С помощью предела монотонной ограниченной последовательности определяется играющее большую роль в математическом анализе число е — основание натуральных логарифмов:
е = limn→∞ (1 + 1/n)n.
Последовательность (1), как уже отмечалось, монотонная и, кроме того, ограничена сверху. Она имеет предел. Мы легко найдем этот предел. Если он равен a, то число а должно удовлетворять равенству a = √(2 + a). Решая это уравнение, получаем a = 2.