Момент инерции
Кто из нас не следил с удивлением и восторгом за тем, как эффектно фигуристы заканчивают свои выступления на ледяной арене? Они начинают вращаться, зафиксировав центр вращения одним коньком и отталкиваясь другим, широко разведя руки в стороны, достигают достаточно большой угловой скорости вращения, а затем быстро прижимают руки к телу. После этого их угловая скорость вращения резко возрастает.
В чем же тут дело? Почему, лишь прижав руки к телу и не прикладывая больше никаких усилий, фигуристу удается резко увеличить угловую скорость своего вращения? Не опровергается ли этим закон сохранения энергии? Конечно, нет. Объяснение описанного явления дает один из разделов ньютоновской механики — динамика твердого тела. Под твердым телом при этом понимается система частиц, взаимные расстояния между которыми не изменяются.
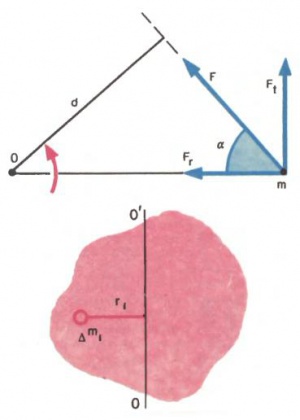
Оказывается, несмотря на сложность задачи о вращательном движении твердого тела, её можно свести к решению уравнений, по форме аналогичных уравнениям Ньютона для поступательного движения. Роль ускорения, силы и массы в этом случае играют угловое ускорение, момент силы и момент инерции. С этими важными понятиями можно познакомиться на простом примере движения одной материальной точки A массой m, которая удерживается на окружности радиуса r с помощью невесомого стержня. Пусть на точку [math]A[/math] действует постоянная сила [math]\overrightarrow{F}.[/math] Если в данный момент она составляет угол [math]α[/math] с радиус-вектором материальной точки [math]A,[/math] то её составляющая [math]F_r=F⋅\cos α[/math] просто сжимает стержень, а составляющая [math]F_t=F⋅\sin α[/math] приводит к появлению тангенциального ускорения [math]a_t,[/math] изменяющего величину скорости частицы. (Это ускорение направлено по касательной к траектории частицы. Его следует отличать от центростремительного ускорения, которое всегда направлено к центру вращения и меняет лишь направление вектора скорости частицы.)
Согласно второму закону Ньютона, для тангенциального ускорения можно записать:
[math]m⋅a_t=F_t=F⋅\sin α.[/math]
По аналогии с угловой скоростью введем угловое ускорение [math]ε=\frac{a_t}{r}.[/math] Оно характеризует скорость изменения угловой скоростиω со временем. Тогда равенство (1) будет иметь вид:
[math]F⋅\sin α=m⋅r⋅\frac{a_t}{r}=m⋅r⋅ε.[/math]
Умножив обе части этого уравнения на радиус, получим:
[math]F⋅r⋅\sin α=m⋅r^2⋅ε,[/math]
или [math]M=J⋅ε.[/math]
Величина [math]M=F⋅r⋅\sin α,[/math] численно равная произведению силы [math]F[/math] на длину перпендикуляра [math]d=r⋅\sin α,[/math] опущенного на направление силы из центра вращения (плечо силы), называется моментом силы относительно точки [math]O.[/math] Величину [math]J=m⋅r^2,[/math] равную произведению массы материальной точки [math]A[/math] на квадрат её расстояния до центра вращения, называют моментом инерции материальной точки относительно точки [math]O.[/math]
В случае произвольного твердого тела момент инерции характеризуется распределением массы в этом теле и определяется суммой моментов инерции совокупности материальных точек, на которые можно разбить твердое тело:
[math]J=\sum\limits_{i=1}^{N}{\Delta {{m}_{i}}r_{i}^{2}},[/math]
где [math]Δm_i[/math] — масса [math]i[/math]‑й точки, [math]r_i[/math] — её расстояние до оси вращения.
<addc>l</addc>
Момент инерции служит мерой инертности тела при вращении и, таким образом, играет ту же роль, что и масса в случае поступательного движения. Однако в отличие от массы тела, которая при обычных условиях остается неизменной, момент инерции можно легко менять. Действительно, даже в рассмотренном выше простейшем случае материальной точки на стержне момент инерции зависел не только от величины массы, но и от того, как далеко она расположена от оси вращения. Поэтому, перемещая материальную точку по стержню от центра вращения, можно увеличивать инерцию вращения такой системы.
В зависимости от формы и выбранной оси вращения твердые тела одной и той же массы могут иметь различные моменты инерции. Так, момент инерции полого цилиндра радиуса [math]r[/math] относительно его оси симметрии равен [math]mr^2;[/math] однородного шара, вращающегося относительно оси, проходящей через его центр, — [math]\frac{2}{5}mr^2;[/math] однородного цилиндра, вращающегося относительно своей оси симметрии, — [math]\frac{1}{2}mr^2.[/math]
И момент силы [math]\overrightarrow{M},[/math] и угловая скорость [math]\overrightarrow{ω},[/math] и угловое ускорение [math]\overrightarrow{ε}[/math] так же как и соответствующие им величины силы, скорости и ускорения при описании поступательного движения, являются векторами. Эти векторы направлены вдоль оси вращения (аксиальные векторы), причем их направление определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения буравчика, рукоятка которого вращается в том же направлении, что и тело.
Можно ввести еще один важный вектор: [math]L=J⋅\overrightarrow{ω},[/math] называемый моментом количества движения. Являясь аналогом импульса для вращательного движения, он обладает замечательным свойством: момент количества движения замкнутой системы остается постоянным по величине и направлению. Изменяется он только под воздействием приложенных к рассматриваемой системе нескомпенсированных моментов внешних сил.
Вернемся снова к началу этой статьи, где рассказывалось о вращающемся фигуристе. Пренебрегая малыми моментами действующих на него сил сопротивления, можно считать, что он представляет собой замкнутую систему. Поэтому достигнутый им при начальном разгоне момент количества движения [math]J_1⋅\overrightarrow{ω_1}[/math] должен сохраняться ([math]ω_1[/math] — его начальная угловая скорость, [math]J_1[/math] — момент инерции в положении с разведенными руками). Прижимая руки к телу, фигурист, очевидно, уменьшает свой момент инерции до некоторой величины [math]J_2[/math] и тем самым увеличивает свою угловую скорость: [math]ω_2=\frac{J_1}{J_2}.[/math] Однако в этот момент ему приходится «поработать», так как начальная кинетическая энергия его вращения была [math]\frac{J_1⋅ω_1^2}{2},[/math] а конечная становится [math]\frac{J_2⋅ω_2^2}{2}.[/math] Разность этих энергий и составляет величину работы фигуриста.