Металлы
Обычно под металлами понимают вещества, хорошо проводящие электрический ток (обладающие малым электросопротивлением). Это действительно самое характерное свойство металлов, которое отличает их от диэлектриков и полупроводников. Но можно ли провести четкую границу между всеми этими группами веществ, основываясь только на величине их электропроводности? Если сравнить удельные сопротивления алюминия — [math]2,5⋅10^{−6}[/math] Ом•см и стекла — [math]10^{12}[/math] Ом•см, то они, действительно, отличаются на много порядков. Ну а как быть с висмутом (его удельное сопротивление [math]1,2⋅10^{−4}[/math] Ом•см) и германием (в чистом виде он имеет сопротивление [math]6⋅10^1[/math] Ом•см, но, вводя специальные примеси, его можно уменьшить на несколько порядков)? Эти вещества по величине электропроводности занимают промежуточное положение между металлами и диэлектриками. Тем не менее можно утверждать, что висмут — металл, а германий — полупроводник.
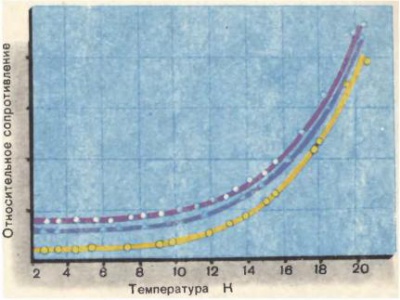
Ответ на вопрос, является ли вещество металлом, дает температурная зависимость сопротивления. У металлов электропроводность остается отличной от нуля даже при очень низких температурах (в пределе и при абсолютном нуле) (рис. [math]1[/math]). В противоположность этому полупроводники перестают проводить электрический ток при нулевой температуре.
Такое отличительное свойство металлов связано с особым характером движения электронов. Электроны подчиняются законам квантовой механики, и их энергия может принимать только определенные дискретные значения. В атомах разрешенные значения (уровни) энергии, как известно, определяются постулатами Бора. Сближая два атома, можно образовать молекулу. При этом каждый атомный уровень энергии расщепляется на два подуровня.
<addc>l</addc>
Чтобы это стало понятным, приведем аналогию с маятником. Каждый маятник имеет одну определенную частоту колебаний [math]ω.[/math] В классической механике его энергия может принимать любые значения, а у квантового осциллятора только дискретные уровни энергии, расстояние между которыми [math]ħω[/math] (в этом смысле он похож на атом). Если связать два одинаковых маятника (соединить, например, пружинкой), то станут возможными два типа колебаний (колебания разных маятников могут быть в фазе или в противофазе), происходящие с разной частотой. В квантовом случае каждый уровень энергии маятника соответственно расщепляется на два подуровня.
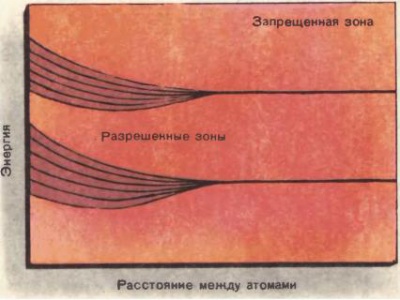
Теперь можно представить, что сближается много атомов (рис. [math]2[/math]). Тогда каждый атомный уровень расщепляется на большое число тесно расположенных подуровней, образующих, как говорят, зону разрешенных значений энергии. Эти зоны разделены областями запрещенных значений энергии (энергетической щелью). Так устроен спектр энергий электронов в твердом теле.
Как заполняют электроны уровни энергии? Согласно принципу Паули, электроны не могут находиться в одинаковых состояниях. Поэтому они не скапливаются на нижнем уровне энергии, а заполняют все более и более высокие уровни.
Максимальная энергия, которой обладают электроны, зависит от их концентрации и называется энергией (уровнем) Ферми. Важно, что в металле уровень Ферми лежит внутри зоны разрешенных значений энергий.
Рассмотрим, например, простейший металл — литий. Каждый атом у него состоит из трех электронов, расположенных на двух оболочках (уровнях энергии): на внутренней — [math]2[/math] электрона, на внешней — недостроенной — [math]1[/math] электрон. При сближении двух атомов лития каждый уровень расщепляется на два подуровня. На нижней паре размещаются [math]4[/math] электрона, а [math]2[/math] — располагаются на нижнем подуровне верхнего расщепленного атомного уровня. Верхний подуровень при этом остается свободным. Легко понять, что если объединить много атомов лития, то верхняя зона разрешенных значений энергии окажется заполненной лишь наполовину.
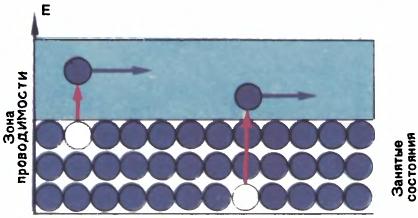
Способность металлов хорошо проводить электрический ток как раз объясняется таким устройством их зонной структуры. Для того чтобы потек электрический ток, электроны должны иметь возможность ускоряться электрическим полем, увеличивать свою энергию. Если зона заполнена не полностью, то энергия электрона может меняться почти непрерывно (электрон при этом переходит на соседний свободный уровень) и электрическое поле легко создает ток (рис. [math]3[/math]). Другое дело, если зона заполнена целиком. Тогда следующий свободный уровень находится далеко — он отделен энергетической щелью, и поле не способно ускорять электроны. В этом случае вещество является диэлектриком. Тепловые возбуждения в диэлектриках могут переводить электроны в верхнюю свободную зону, но число таких возбужденных электронов очень мало.
Движение электронов в металле похоже на движение свободных частиц. Каждый атом отдает один или несколько электронов в коллективное пользование. Хотя эти электроны двигаются сквозь кристаллическую решетку, состоящую из плотно упакованных ионов, они ведут себя почти как свободные частицы. Волны, описывающие в квантовой механике состояние электронов, при периодическом расположении ионов распространяются, как в прозрачной среде, не затухая. При этом всё влияние кристаллической решетки сводится к изменению массы электрона — в металле он обладает эффективной массой, отличной от массы свободного электрона.
Импульс электрона в металле, так же как и энергия, принимает дискретный ряд значений. В состоянии с заданным импульсом могут находиться только [math]2[/math] электрона с противоположно направленными спинами (принцип Паули). Максимальный импульс электронов называется импульсом Ферми.
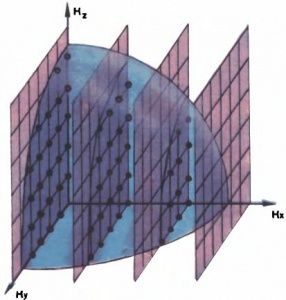
Поскольку энергия электрона пропорциональна квадрату импульса ([math]E=\overrightarrow{p}^2/2m[/math]), то электроны при абсолютном нуле занимают все возможные состояния в сфере радиуса [math]p_F[/math] (рис. [math]4[/math]). Эта сфера называется поверхностью Ферми. Взаимодействие электронов с кристаллической решеткой в некоторых случаях может привести к сложной форме поверхности Ферми (рис. [math]5[/math]) и к нарушению закона [math]E=\overrightarrow{p}^2/2m.[/math]
Энергия Ферми в хороших металлах — очень большая величина. Она соответствует энергии теплового движения электронов при температурах в несколько тысяч градусов! Поэтому при обычных температурах «размытие» поверхности Ферми вследствие тепловых возбуждений невелико. Этим обстоятельством объясняется сравнительно малая величина теплоемкости электронов. Если бы электроны подчинялись классическим законам, то молярная теплоемкость электронного газа равнялась бы [math]3R/2[/math] и добавлялась к теплоемкости кристаллической решетки [math]3R,[/math] чего на опыте никогда не наблюдается. Лишь очень малая часть электронов вблизи поверхности Ферми способна возбуждаться при нагревании, и их теплоемкость обычно составляет только проценты от теплоемкости решетки.
Тепловые колебания ионов (см. Фонон), примеси и дефекты нарушают регулярность в расположении ионов и препятствуют свободному движению электронов в металле. При понижении температуры сопротивление металлов обычно уменьшается, а при низких температурах оно становится постоянным и определяется рассеянием электронов на примесях и дефектах.
Любопытно, что если сильно «испортить» металл, загрязнить его примесями, то при охлаждении он может стать диэлектриком: электроны локализуются вблизи примесей, и проводимость при абсолютном нуле оказывается равной нулю (а сопротивление бесконечным). Такой эффект особенно сильный в тонких пленках или проволочках. Существует комбинация мировых постоянных: [math]R_0=h/e^2=26[/math] кОм, которая имеет размерность сопротивления и определяет необходимую степень загрязнения металла. Образцы, имеющие сопротивление большее, чем [math]R_0,[/math] при охлаждении должны становиться диэлектриками. Правда, температура перехода в диэлектрическое состояние сильно зависит от размера образца (толщины пленки или диаметра проволоки). Наблюдать этот эффект удалось только на очень тонких металлических проволоках и пленках.