Магические и латинские квадраты
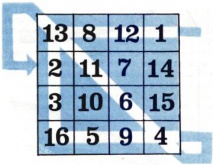
Если внимательно присмотреться к числам от [math]1[/math] до [math]16,[/math] расположенным в клетках квадрата на рис. 1, то можно заметить следующую закономерность: сумма чисел в каждом горизонтальном ряду, в каждом вертикальном ряду и по каждой из диагоналей одна и та же. Такой квадрат и все квадраты, обладающие аналогичным свойством, получили название магических.
<addc>l</addc>
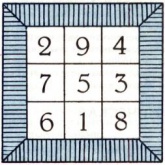
Задачи составления и описания магических квадратов интересовали математиков с древнейших времен. Однако полного описания всех возможных магических квадратов не получено и до сего времени. Магических квадратов [math]2×2[/math] не существует. На рис. 2 изображен единственный магический квадрат [math]3×3.[/math] Единственный в том смысле, что все остальные магические квадраты [math]3×3[/math] получаются из него либо поворотом вокруг центра, либо отражением относительно одной из его осей симметрии.
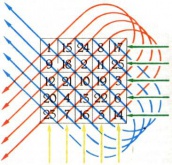
С увеличением размеров (числа клеток) квадрата быстро растет количество возможных магических квадратов. Так, например, различных магических квадратов [math]4×4[/math] уже [math]880,[/math] а для размера [math]5×5[/math] их количество приближается к четверти миллиона. Среди них есть квадраты, обладающие интересными свойствами. Например, в квадрате на рис. 3 равны между собой не только суммы чисел в строках, столбцах и диагоналях, но и суммы пятерок чисел по «разломанным» диагоналям, связанным на рисунке цветными линиями.
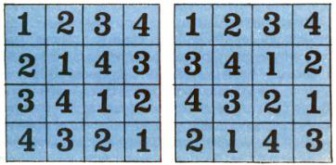
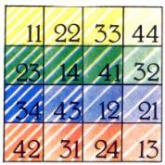
Латинским квадратом называется квадрат [math]n×n[/math] клеток, в которых написаны числа [math]1,\ 2,\ …,\ n,[/math] притом так, что в каждой строке и каждом столбце встречаются все эти числа по одному разу. На рис. 4 изображены два таких латинских квадрата [math]4×4.[/math] Они обладают интересной особенностью: если один квадрат наложить на другой, то все пары получившихся чисел оказываются различными. Такие пары латинских квадратов называются ортогональными. Задачу отыскания ортогональных латинских квадратов впервые поставил Л. Эйлер, причем в такой занимательной формулировке: «Среди [math]36[/math] офицеров поровну уланов, драгунов, гусаров, кирасиров, кавалергардов и гренадеров и, кроме того, поровну генералов, полковников, майоров, капитанов, поручиков и подпоручиков, причем каждый род войск представлен офицерами всех шести рангов. Можно ли выстроить этих офицеров в каре [math]6×6[/math] так, чтобы в любой колонне и любой шеренге встречались офицеры всех рангов?»
Эйлер не смог найти решения этой задачи. В 1901 г. было доказано, что такого решения не существует. В то же время Эйлер доказал, что ортогональные пары латинских квадратов существуют для всех нечетных значений [math]n[/math] и для таких четных значений [math]n,[/math] которые делятся на [math]4.[/math] Решение задачи Эйлера для [math]25[/math] офицеров изображено на рис. 5. Чин офицера символизирует цветной кружок в углу каждой из клеток. Здесь особенно хорошо видна связь между. задачей Эйлера и латинскими квадратами: рода войск соответствуют числам одного латинского квадрата, а чины (цветные точки) — числам ортогонального ему латинского квадрата. Эйлер выдвинул гипотезу, что для остальных значений и, т. е. если число [math]n[/math] при делении на [math]4[/math] дает в остатке [math]2,[/math] ортогональных квадратов не существует. В 1901 г. было доказано, что ортогональных квадратов размером [math]6×6[/math] не существует, и это усиливало уверенность в справедливости гипотезы Эйлера. Однако в 1959 г. с помощью компьютера были найдены сначала ортогональные квадраты [math]10×10,[/math] потом [math]14×14,[/math] [math]18×18,[/math] [math]22×22.[/math] А затем было показано, что для любого [math]n,[/math] кроме [math]6,[/math] существуют ортогональные квадраты размером [math]n×n.[/math]
Магические и латинские квадраты — близкие родственники. Пусть мы имеем два ортогональных латинских квадрата. Заполним клетки нового квадрата тех же размеров следующим образом. Поставим туда число [math]n(a−1)+b,[/math] где [math]a[/math] — число в такой клетке первого квадрата, а [math]b[/math] — число в такой же клетке второго квадрата. Нетрудно понять, что в полученном квадрате суммы чисел в строках и столбцах (но не обязательно на диагоналях) будут одинаковы.
Теория латинских квадратов нашла многочисленные применения как в самой математике, так и в её приложениях. Приведем такой пример. Пусть мы хотим испытать [math]4[/math] сорта пшеницы на урожайность в данной местности, причем хотим учесть влияние степени разреженности посевов и влияние двух видов удобрений. Для этого разобьем квадратный участок земли на [math]16[/math] делянок (рис. 6). Первый сорт пшеницы посадим на делянках, соответствующих нижней горизонтальной полосе, следующий сорт — на четырех делянках, соответствующих следующей полосе, и т. д. (на рисунке сорт обозначен цветом). При этом максимальная густота посевов пусть будет на тех делянках, которые соответствуют левому вертикальному столбцу рисунка, и уменьшается при переходе вправо (на рисунке этому соответствует уменьшение интенсивности цвета). Цифры же, стоящие в клетках рисунка, пусть означают: первая — количество килограммов удобрения первого вида, вносимого на этот участок, а вторая — количество вносимого удобрения второго вида. Эти числа на [math]1[/math] меньше чисел в ортогональных латинских квадратах из рис. 4. Нетрудно понять, что при этом реализованы все возможные пары сочетаний как сорта, и густоты посева, так и других компонентов: сорта и удобрений первого вида, удобрений первого и второго видов, густоты и удобрений второго вида.
Использование ортогональных латинских квадратов помогает учесть все возможные варианты в экспериментах в сельском хозяйстве, физике, химии, технике.