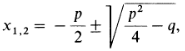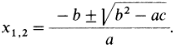Квадратное уравнение
Квадратным называют алгебраическое уравнение 2‑й степени, т. е. уравнение вида
[math]a{{x}^{2}}+bx+c=0[/math], где [math]a\ne 0[/math].
Выражение [math]D={{b}^{2}}-4ac[/math] называют дискриминантом квадратного трехчлена [math]a{{x}^{2}}+bx+c[/math]. Уравнение (1) имеет два корня:
При этом если D > 0, то корни действительные и различные, при D = 0 корни совпадают (говорят, что уравнение имеет корень кратности два), при D < 0 корни комплексные (комплексно сопряженные). Для приведенного квадратного уравнения
x2 + px + q = 0
формула корней имеет вид
а для уравнения ax2 + 2bx + c = 0 (с четным коэффициентом при x) — вид
Для коэффициентов и корней квадратного уравнения (1) выполняются соотношения:
Эти соотношения называют теоремой Виета, по имени французского математика Ф. Виета (1540–1603).
Особенно удобна эта теорема для приведенного квадратного уравнения:
x1 + x2 = −p, x1x2 = q.
Уравнения 2‑й степени умели решать еще в Древнем Вавилоне во II тысячелетии до н. э. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид — при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактатах. Приведем задачу из китайского трактата «Математика в девяти книгах» (приблизительно II в. до н. э.).
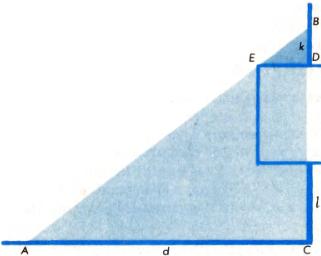
«Имеется город с границей в виде квадрата со стороной неизвестного размера, в центре каждой стороны находятся ворота. На расстоянии 20 бу (1 бу = 1,6 м) от северных ворот (вне города) стоит столб. Если пройти от южных ворот 14 бу прямо, затем повернуть на запад и пройти еще 1 775 бу, то можно увидеть столб. Спрашивается: какова сторона границы города?» Обозначим сторону квадрата через x. Из подобия треугольников BED и ABC (рис. 1) получим
k/(0.5x) = (k + x + l)/d
Поэтому, чтобы определить неизвестную сторону квадрата, получаем квадратное уравнение
x2 + (k + l)x − 2kd = 0.
В данном случае уравнение имеет вид
x2 + 34x − 71 000 = 0,
откуда x = 250 (бу).
Отрицательных корней (в данном случае x = −284) китайские математики не рассматривали, хотя в этом же трактате содержатся операции с отрицательными числами.
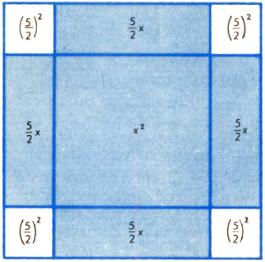
Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы принадлежит индийскому математику Брахмагупте (около 598 г.). Среднеазиатский ученый аль‑Хорезми (IX в.) в трактате «Китаб аль‑джебр валь‑мукабала» получил эту формулу методом выделения полного квадрата с помощью геометрической иллюстрации. Суть его рассуждений видна из рис. 2 (он рассматривает уравнение x2 + 10x = 39). Площадь большого квадрата равна (x + 5)2. Она складывается из площади x2 + 10x фигуры, закрашенной голубым цветом, равной левой части рассматриваемого уравнения, и площади четырех квадратов со стороной 5/2, равной 25. Таким образом,
(x + 5)2 = 39 + 25; x + 5 = ±8; x1 = 3; x2 = −13.
К квадратным уравнениям сводятся многие уравнения путем замены переменной.
Приведем некоторые примеры.
1. Биквадратное уравнение
ax4 + bx2 + c = 0
сводится к квадратному заменой x2 переменной y.
2. Уравнение (x + 1)2 − 6/(x2 + 2x) = −4 заменой y = x2 + 2x сводится к квадратному уравнению y2 + 5y − 6 = 0, корни которого y1 = 1, y2 = −6. Из двух уравнений x2 + 2x = 1 и x2 + 2x = −6 действительные решения имеет только первое: x = −1 + √2.
3. Уравнения
4x − 2x + 1 − 3 = 0, cos 2x = sin x + 1, lg2(x2) + lg x = 1
сводятся к квадратным заменами соответственно y = 2x, y = sin x и y = lg x.
4. Уравнение
x2/3 + 48/x2 = 10(x/3 + 4/x)
сводится к квадратному уравнению заменой
y = x/3 + 4/x (здесь x2/3 + 48/x2 = 3(x/3 + 4/x)2 − 8 = 3y2 − 8; 3y2 − 10y − 8 = 0; y1 = −2/3, y2 = 4).
Из получаемых уравнений
x/3 + 4/x = −2/3 и x/3 + 4/x = 4
корни имеет только второе: x = 2(3 ± √6). Вообще, замена y = x + k/x — одна из наиболее часто встречающихся замен. Например, с помощью такой замены к квадратному уравнению (после деления обеих частей уравнения на x2) сводится уравнение вида
ax4 + bx3 + cx2 + kbx + k2a = 0.
Уравнение (2) обычно называют возвратным или обобщенно-симметрическим.
5. Однородные уравнения
9x = 6x + 2•4x и 2sin2x + 5 sin x cos x + 2cos2x = 0 сводятся к квадратным уравнениям относительно y заменами соответственно y = (3/2)x и y = tg x после деления обеих частей первого уравнения на 4x, второго — на cos2x. Для второго уравнения предварительно проверяется, удовлетворяют ли уравнению те значения x, для которых cos x = 0.
6. Уравнение
x4 + (x + 2)4 = 82,
«симметричное» относительно x + 1, сводится к биквадратному уравнению y4 + 6y2 = 40 заменой y = x + 1; аналогично уравнение (x + 1)(x + 2)(x + 4)(x + 5) = 40, «симметричное» относительно x + 3, сводится к биквадратному уравнению (y2 − 1)(y2 − 4) = 40 заменой y = x + 3. Отметим, что для второго уравнения годится и замена y = x2 + 6x, тогда (x + 1)(x + 5) = y + 5; (x + 2)(x + 4) = y + 8.